
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3

a: Thay \(x=9+4\sqrt{2}\) vào A, ta được:
\(A=\dfrac{2\sqrt{2}+1+7}{2\sqrt{2}+1-1}=\dfrac{8+2\sqrt{2}}{2\sqrt{2}}=2\sqrt{2}+1\)



Bài 3:
Gọi K là giao của AH và BC thì AK là đường cao thứ 3 (H là trực tâm)
Vì \(\widehat{BDC}=\widehat{BEC}=90^0\) nên BEDC nội tiếp
Lại có \(BI=IC=ID=IE=\dfrac{1}{2}BC\) (trung tuyến ứng cạnh huyền) nên I là tâm đg tròn ngoại tiếp BDEC
Gọi G là trung điểm AH thì \(AG=GD=DE=\dfrac{1}{2}AH\) (trung tuyến ứng ch)
Do đó G là tâm () ngoại tiếp tg ADE
Vì \(GA=GD\Rightarrow\widehat{DAG}=\widehat{GDA}\)
Vì \(ID=IB\Rightarrow\widehat{ABI}=\widehat{IDB}\)
Do đó \(\widehat{IDB}+\widehat{GDA}=\widehat{DAG}+\widehat{ABI}=90^0\left(\Delta AKB\perp K\right)\)
Do đó \(\widehat{IDG}=180^0-\left(\widehat{IDB}+\widehat{GDA}\right)=90^0\)
Vậy \(ID\perp IG\) hay ...









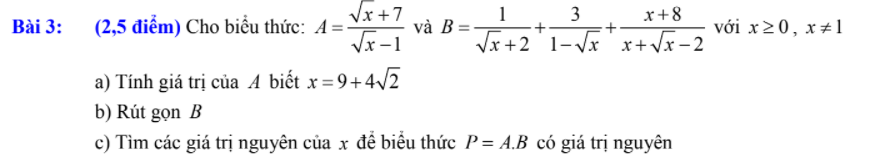 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 

