Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
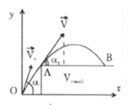
Để viên bi có thể rơi xa mép bàn A nhất thì quỹ đạo của viên bi phải sát A.
Gọi vận tốc viên bi tại A là v m/s.
A B max ⇔ α 1 = 45 0
( α 1 là góc hợp bởi AB và vận tốc tại A).
Do theo phương Ox viên bi chuyển động đều nên các vận tốc thành phần bằng nhau:
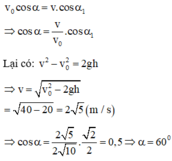

Phương trình chuyển động ném xiên của viên bi:
Theo trục Ox: \(x=\left(v_0\cos\alpha\right)t\)
Theo trục Oy: \(y=\left(v_0\sin\alpha\right)t-\dfrac{1}{2}gt^2\)
Phương trình quỹ đạo của viên bi: \(y=\dfrac{-g}{2v_0^2\cos^2\alpha}x^2+\left(\tan\alpha\right)x\)
Để tầm xa trên mặt bàn cực đại thì viên bi phải bay sát mép bàn và hợp với phương ngang 1 góc 45 độ
Dễ chứng minh: \(\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\)
Chứng minh: Ta có: \(v_x=v_y\Leftrightarrow v^2x=v^2y\) (1)
\(v^2x=v_0^2\cos^2\alpha\left(2\right)\) và \(v^2y-v_0^2\sin^2\alpha=-2gh\Rightarrow v^2y=-2gh+v_0^2\sin^2\alpha\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow v_0^2\cos^2\alpha=v_0^2\sin^2\alpha-2gh\Rightarrow\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\) ( Done :D )
Tại mặt bàn: \(y=h\Leftrightarrow-\dfrac{g}{2v_0^2\cos^2\alpha}x^2+\left(\tan\alpha\right)x=h\left(4\right)\)
(4) có 2 nghiệm x1 < x2
Gọi x1 là khoảng cách từ chỗ ném viên bi đến chân bàn H
x2 là tầm xa cực đại trên mặt bàn của viên bi
\(\left(4\right)\Leftrightarrow x=\dfrac{v_0^2}{g}\left(\sin\alpha\cos\alpha\pm\dfrac{\cos\alpha\sqrt{v_0^2\sin^2\alpha-2gh}}{v_0}\right)\)
Ta đã chứng minh được: \(\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\) \(\Rightarrow\sin\alpha=\sqrt{\dfrac{1}{2}+\dfrac{gh}{v_0^2}}\)
\(\Rightarrow x_1=\dfrac{v_0^2}{g}\left[-\dfrac{1}{2}+\dfrac{gh}{v_0^2}+\sqrt{\dfrac{1}{4}-\left(\dfrac{gh}{v_0^2}\right)^2}\right]\)
\(\Rightarrow x_2=\dfrac{v_0^2}{g}\left[\dfrac{1}{2}-\dfrac{gh}{v_0^2}+\sqrt{\dfrac{1}{4}\left(\dfrac{gh}{v_0^2}\right)^2}\right]\)
Vậy......

a. Chọn mốc Wt tại mặt đất.
Bỏ qua sức cản của không khí => cơ năng được bảo toàn.
Gọi vị trí ném vật là A
WtA=m.g.hA = 0,05.10.10 = 5 (J)
WđA=\(\dfrac{1}{2}\).m.vA2=\(\dfrac{1}{2}\).0,05.102=\(\dfrac{5}{2}\)(J)
b.Gọi vị trí vật chạm đất là B.
WB=WA= WtA + WđA = \(\dfrac{15}{2}\)(J)
Khi đó WtB = 0 (J)
=> WđB = \(\dfrac{15}{2}\)
=> \(\dfrac{1}{2}\).m.vB2 = \(\dfrac{1}{2}\).0,05.vB2=\(\dfrac{15}{2}\)
<=> vB = 10\(\sqrt{3}\)(m/s)
c. Gọi độ cao cực đại mà vật có thể đạt được so với mặt đất là C, khi đó vC=0 (m/s) <=> WđC=0
WC=WA=7,5=WtC
<=> m.g.hC=7,5
<=> 0,05.10.hC=7,5
<=> hC = 15 (m)
d. Gọi vị trí Wđ = 2Wt là D
Khi đó \(\dfrac{1}{2}\).m.vD2 = 2.m.g.hD
WD = WA = 7,5
=> \(\dfrac{1}{2}\).m.vD2 + m.g.hD = 7,5
<=> 3.m.g.hD = 7.5
<=> hD = 5(m)
Khi đó vD = 10\(\sqrt{2}\)(m/s) (Thay hD vào rồi tính được vD nhé)
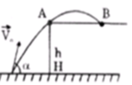
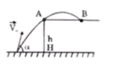

Đáp án: C
Để viên bi có thể rơi xa mép bàn A nhất thì quỹ đạo của viên bi phải sát A.
Gọi vận tốc viên bi tại A là v m/s.
Do theo phương Ox viên bi chuyển động đều nên các vận tốc thành phần bằng nhau:
Lại có: