Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
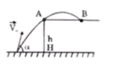
Để viên bi có thể rơi xa mép bàn A nhất thì quỹ đạo của viên bi phải sát A.
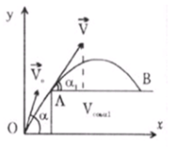
Gọi vận tốc viên bi tại A là v m/s.
![]() là góc hợp bởi AB và vận tốc tại A).
là góc hợp bởi AB và vận tốc tại A).
Do theo phương Ox viên bi chuyển động đều nên các vận tốc thành phần bằng nhau:
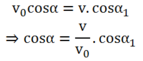
Lại có:
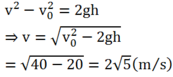
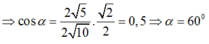

Phương trình chuyển động ném xiên của viên bi:
Theo trục Ox: \(x=\left(v_0\cos\alpha\right)t\)
Theo trục Oy: \(y=\left(v_0\sin\alpha\right)t-\dfrac{1}{2}gt^2\)
Phương trình quỹ đạo của viên bi: \(y=\dfrac{-g}{2v_0^2\cos^2\alpha}x^2+\left(\tan\alpha\right)x\)
Để tầm xa trên mặt bàn cực đại thì viên bi phải bay sát mép bàn và hợp với phương ngang 1 góc 45 độ
Dễ chứng minh: \(\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\)
Chứng minh: Ta có: \(v_x=v_y\Leftrightarrow v^2x=v^2y\) (1)
\(v^2x=v_0^2\cos^2\alpha\left(2\right)\) và \(v^2y-v_0^2\sin^2\alpha=-2gh\Rightarrow v^2y=-2gh+v_0^2\sin^2\alpha\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow v_0^2\cos^2\alpha=v_0^2\sin^2\alpha-2gh\Rightarrow\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\) ( Done :D )
Tại mặt bàn: \(y=h\Leftrightarrow-\dfrac{g}{2v_0^2\cos^2\alpha}x^2+\left(\tan\alpha\right)x=h\left(4\right)\)
(4) có 2 nghiệm x1 < x2
Gọi x1 là khoảng cách từ chỗ ném viên bi đến chân bàn H
x2 là tầm xa cực đại trên mặt bàn của viên bi
\(\left(4\right)\Leftrightarrow x=\dfrac{v_0^2}{g}\left(\sin\alpha\cos\alpha\pm\dfrac{\cos\alpha\sqrt{v_0^2\sin^2\alpha-2gh}}{v_0}\right)\)
Ta đã chứng minh được: \(\cos\alpha=\sqrt{\dfrac{1}{2}-\dfrac{gh}{v_0^2}}\) \(\Rightarrow\sin\alpha=\sqrt{\dfrac{1}{2}+\dfrac{gh}{v_0^2}}\)
\(\Rightarrow x_1=\dfrac{v_0^2}{g}\left[-\dfrac{1}{2}+\dfrac{gh}{v_0^2}+\sqrt{\dfrac{1}{4}-\left(\dfrac{gh}{v_0^2}\right)^2}\right]\)
\(\Rightarrow x_2=\dfrac{v_0^2}{g}\left[\dfrac{1}{2}-\dfrac{gh}{v_0^2}+\sqrt{\dfrac{1}{4}\left(\dfrac{gh}{v_0^2}\right)^2}\right]\)
Vậy......

\(v^2-v_o^2=2gh\)
\(\Leftrightarrow0-10^2=2\cdot\left(-10\right)h\)
\(\Leftrightarrow h=5\left(m\right)\)

Áp dụng định luật bảo toàn cơ năng ta có Wmặt đất=Wvị trí cực đại
<=>m*v^2/2=m*g*z<=>100=20*z<=>z=5
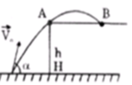

Đáp án C
Để viên bi có thể rơi xa mép bàn A nhất thì quỹ đạo của viên bi phải sát A.
Gọi vận tốc viên bi tại A là v m/s.
A B max ⇔ α 1 = 45 0
( α 1 là góc hợp bởi AB và vận tốc tại A).
Do theo phương Ox viên bi chuyển động đều nên các vận tốc thành phần bằng nhau: