e đg cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp e với,sắp thi r
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
5.
Tọa độ dỉnh của (P) là: \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\Rightarrow I\left(1;-4m-2\right)\)
Để I thuộc \(y=3x-1\)
\(\Rightarrow-4m-2=3.1-1\)
\(\Rightarrow m=-1\)
6.a.
Với \(a\ne0\)
\(\left\{{}\begin{matrix}64a+8b+c=0\\-\dfrac{b}{2a}=5\\\dfrac{4ac-b^2}{4a}=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}64a+8b+c=0\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-64a-8b=-64a-8\left(-10a\right)=16a\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Rightarrow4a.16a-\left(-10a\right)^2=48a\)
\(\Rightarrow a=-\dfrac{4}{3}\Rightarrow b=\dfrac{40}{3}\Rightarrow c=-\dfrac{64}{3}\)
Hay pt (P): \(y=-\dfrac{4}{3}x^2+\dfrac{40}{3}x-\dfrac{64}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
b.
Thay tọa độ 3 điểm vào pt (P) ta được:
\(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\)
Pt (P): \(y=x^2-x-1\)
c.
Do (P) đi qua 3 điểm có tọa độ (1;16); (-1;0); (5;0) nên ta có:
\(\left\{{}\begin{matrix}a+b+c=16\\a-b+c=0\\25a+5b+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=8\\c=10\end{matrix}\right.\)
hay pt (P) có dạng: \(y=-2x^2+8x+10\)
mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha
DM
21 tháng 4 2017
Box toán 10 hình như phóng đại quá bạn ơi :v
Câu 2 bạn tự giải và biểu diễn nghiệm nhé, mình k biết vẽ biểu diễn :V
Bài 3 :
a) \(\left|2x+1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=5\left(2x+1\ge0\right)\\-\left(2x+1\right)=5\left(2x+1< 0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=4\left(x\ge-\dfrac{1}{2}\right)\\-2x-1=5\left(x< -\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(x\ge-\dfrac{1}{2}\right)\left(TMĐK\right)\\x=-3\left(x< -\dfrac{1}{2}\right)\left(TMĐK\right)\end{matrix}\right.\)
Vậy \(S=\left\{-3;2\right\}\)
b) \(\left|x\right|=2x+1\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2x+1\left(x\ge0\right)\\-x=2x+1\left(x< 0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(x\ge0\right)\left(KTMĐK\right)\\x=-\dfrac{1}{3}\left(x< 0\right)\left(TMĐK\right)\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{1}{3}\right\}\)
c) \(\left|2x-5\right|=x-1\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=x-1\left(2x-5\ge0\right)\\-\left(2x-5\right)=x-1\left(2x-5< 0\right)\end{matrix}\right.\)
Giải giống trên : \(\Leftrightarrow\left[{}\begin{matrix}x=4\left(x\ge\dfrac{5}{2}\right)\left(TMĐK\right)\\x=2\left(x< \dfrac{5}{2}\right)\left(TMĐK\right)\end{matrix}\right.\)
Vậy \(S=\left\{2;4\right\}\)
d) \(\left|x+4\right|=2x-5\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=2x-5\left(x\ge-4\right)\\-\left(x+4\right)=2x-5\left(x< -4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\left(TMĐK\right)\\x=\dfrac{1}{3}\left(KTMĐK\right)\end{matrix}\right.\)
Vậy \(S=\left\{9\right\}\)
DM
21 tháng 4 2017
Bài 4 : \(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(A=\left(\dfrac{x}{\left(x+2\right)\left(x-2\right)}-\dfrac{2}{x-2}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(A=\left(\dfrac{x-2x-4+x-2}{\left(x+2\right)\left(x-2\right)}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(A=\dfrac{-6}{\left(x+2\right)\cdot\left(x-2\right)}:\left(\dfrac{x^2-4}{x+2}+\dfrac{10-x^2}{x+2}\right)\)
\(A=\dfrac{-6}{\left(x+2\right)\left(x-2\right)}:\dfrac{6}{x+2}\)
\(A=\dfrac{-6\cdot\left(x+2\right)}{6\left(x+2\right)\left(x-2\right)}=\dfrac{-1}{x-2}\)
b) \(\left|x\right|=\dfrac{1}{2}\Rightarrow x=\left[{}\begin{matrix}-\dfrac{1}{2}\\\dfrac{1}{2}\end{matrix}\right.\)\(\Rightarrow A=\left[{}\begin{matrix}\dfrac{-1}{x-2}=-\dfrac{1}{2}\\\dfrac{-1}{x-2}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)
Vậy \(S=\left\{0;4\right\}\)
c) \(A< 0\Leftrightarrow\dfrac{-1}{x-2}< 0\Rightarrow x-2>-1\Rightarrow x>1\)
Mà mẫu của biểu thức A = x - 2 => Loại số 2 vào danh sách nghiệm.
Vậy để A < 0 thì x > 2.
CD
0
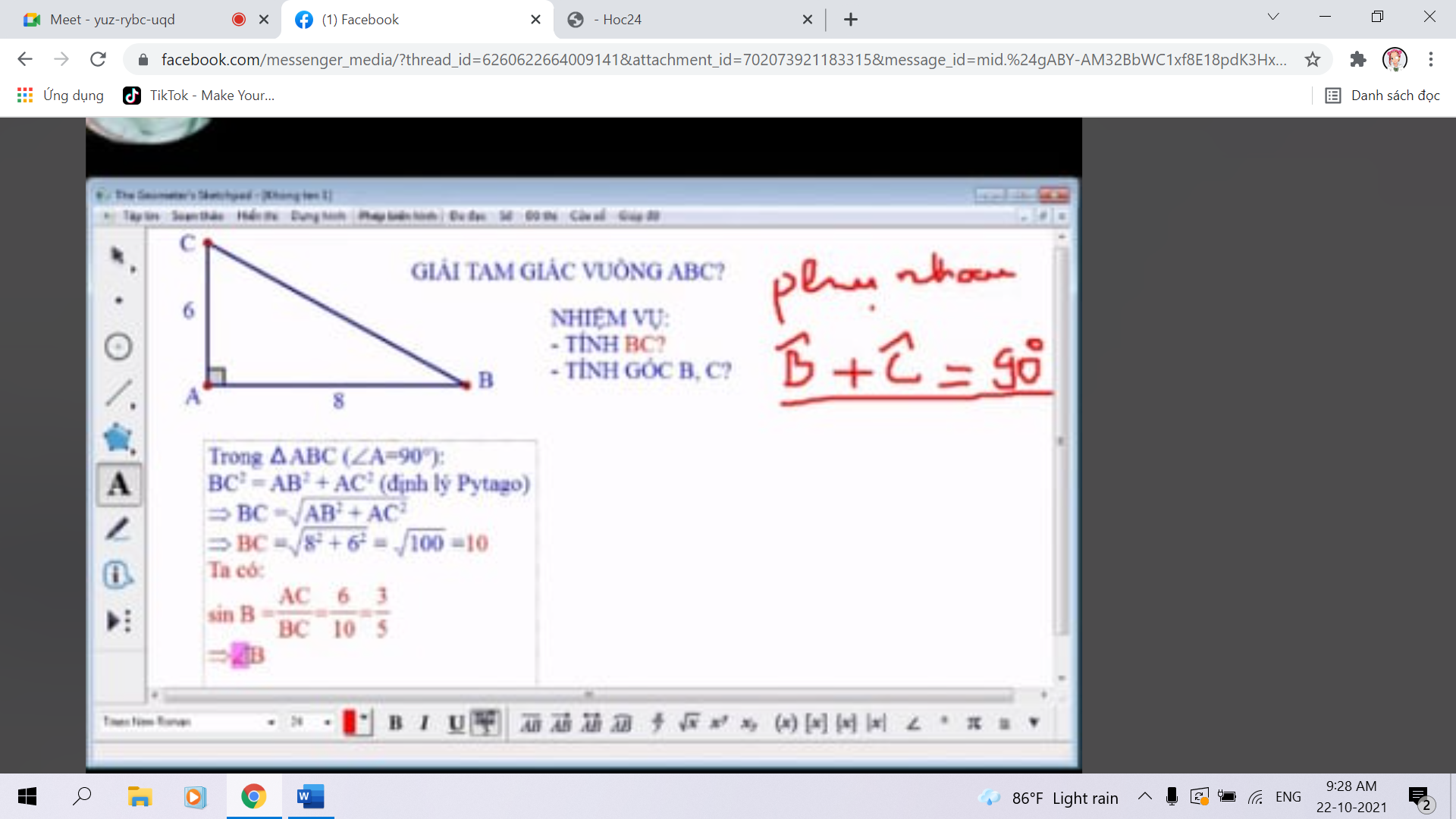
\(\widehat{B}\simeq37^0;\widehat{C}=53^0\)