Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A O B H M K P C
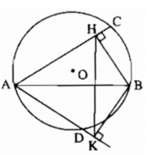
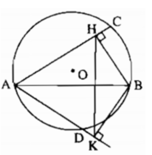
Ta có : \(AH\perp CD\left(gt\right)\)
\(BK\perp CD\left(gt\right)\)
=> AH // BK
=> Tứ giác ABKH là hình thang có đáy AH và BK
Theo ( gt ) : OA = OB mà \(OM\perp CD\)( theo cách dựng )
=> OM // AC / BK
=> MK = MH (1)
Mặt khác : \(OM\perp CD\Rightarrow MC=MD\left(2\right)\)
Từ (1) và (2) => MH - MC = MK - MD
=> CH = DK
Vậy CH = DK

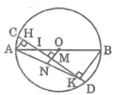
Kẻ OM ⊥ CD cắt AD tại N
Ta có: MC = MD (đường kính dây cung)
Hay MH + CH = MK + KD (1)
Ta có: OM // BK (cùng vuông góc với CD)
Hay: MN // BK
Mà: OA = OB (= R)
Suy ra: NA = NK (tính chất đường trung bình của tam giác)
Lại có: OM // AH (cùng vuông góc với CD)
Hay: MN // AH
Mà: NA = NK (chứng minh trên)
Suy ra: MH = MK (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: CH = DK

Gọi G là giao điểm của AH và EF
Tứ giác AEHF là hình chữ nhật => AH = EF
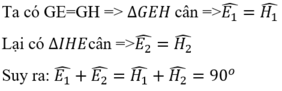
Do đó EF là tiếp tuyến của đường tròn (I)
Tương tự, EF là tiếp tuyến của đường tròn (K)