Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1.
theo phương pháp tổng hợp hai lực song song cùng chiều
\(F=F_1+F_2=24N\Rightarrow F_2=24-F_1=6N\) và
\(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\)\(\Leftrightarrow\dfrac{18}{6}=\dfrac{d_2}{30-d_2}\Rightarrow d_2=22,5cm\)
2.
. T N P -P
a)
\(sin\alpha=\dfrac{T}{P}\Rightarrow T=m.g.sin\alpha=\)24,5N
b)\(cos\alpha=\dfrac{N}{P}\Rightarrow N=\dfrac{49\sqrt{3}}{2}N\)
chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F
Fms=\(\mu\).N
N=\(P-sin\alpha.F=\)\(20-10\sqrt{2}\)N
\(\Rightarrow F_{ms}=\)\(4-2\sqrt{2}\)N
công của lực ma sát
\(A_{F_{ms}}=F_{ms}.s.cos180^0\)=\(-8+4\sqrt{2}\)J
Vì vật chuyển động đều
\(\Rightarrow\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
Chọn trục toạ độ có trục hoành hướng sang phải, trục tung hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:F.\cos\alpha-F_{ms}=0\\Oy:F.\sin\alpha+N-P=0\end{matrix}\right.\)
\(\Rightarrow F.\cos\alpha-\mu.\left(P-F.\sin\alpha\right)=0\)
\(\Leftrightarrow120.\cos60-\mu.\left(200-120.\sin60\right)=0\)
=> \(\mu=...\)
Tìm gia tốc trong trường hợp alpha= 300 thì lúc này vật chuyển động biến đổi đều nên có gia tốc, tức là \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Cậu chiếu lên trục toạ độ rồi phân tích, bt hệ số ma sát rồi thì tìm a ez
a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(cos\alpha.F-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-sin\(\alpha\).F (3)
từ (2),(3) và để vật chuyển động với a=0,5
\(\Rightarrow F\approx\)19N
b) sau 3s lực kéo biến mất
theo định luật II niu tơn
\(\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m.\overrightarrow{a'}\) (*)
chiếu (*) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(-\mu.N=m.a'\) (4)
chiếu (*) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
\(N=P-sin\alpha\) (5)
từ (4),(5)
\(\Rightarrow a'\approx-2,46\)m/s2
ngay sau khi lực F biến mất vận tốc vật lúc đó là
v=a.t=1,5m/s2
thời gian vật đi được đến khi dừng kể từ lúc lực F biến mất
t=\(\dfrac{v_1-v}{a'}\approx0,6s\)
a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F.cos\(\alpha\)-\(\mu.N=0\) (1) (a=0, vật chuyển động đều)
chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-\(sin\alpha.F\) (2)
từ (1),(2)\(\Rightarrow F\approx103,5N\)
b) từ câu a ta có
\(F.cos\alpha-\mu.\left(P-sin\alpha.F\right)=0\)
\(\Leftrightarrow F=\dfrac{\mu.P}{cos\alpha+\mu.sin\alpha}\)
đặt \(\mu\)=\(tan\beta=\dfrac{sin\beta}{cos\beta}\) (\(0^0< \beta< 90^0\)
để F min thì MS= \(cos\alpha+\mu.sin\alpha\) max (MS: mẫu số)
\(\Leftrightarrow\)MS=\(\dfrac{cos\alpha.cos\beta+sin\beta.sin\alpha}{cos\beta}\)=\(\dfrac{cos\left(\alpha-\beta\right)}{cos\beta}\)
MS max khi \(cos\left(\alpha-\beta\right)\)=1 (vì \(cos\beta\) ở dưới mẫu min thì MS max nhưng cos\(\beta\) min ko xác định được )
\(cos\left(\alpha-\beta\right)=1\Leftrightarrow\alpha-\beta=0\)
\(\Leftrightarrow\alpha=\beta\)
\(\Rightarrow tan\alpha=tan\beta=\mu=0,2\)
\(\Rightarrow\alpha\approx11,3^0\)
1.
Ta có: biểu thức định luật 2 Newton: \(\overrightarrow a = \frac{{\overrightarrow F }}{m}\)
\( \Rightarrow \overrightarrow F = m.\overrightarrow a \)
Suy ra cách viết đúng là C.
2.
Theo bài ra, ta có: \(\left\{ \begin{array}{l}m = 0,5kg;\,{v_0} = 0\left( {m/s} \right)\\F = 250N\\t = 0,020{\rm{s}}\end{array} \right.\)
Áp dụng định luật 2 Newton, gia tốc của chuyển động là:
\(a = \frac{F}{m} = \frac{{250}}{{0,5}} = 500\left( {m/{s^2}} \right)\)
Quả bóng bay đi với tốc độ là:
\(v = {v_0} + at = 0 + 500.0,020 = 10\left( {m/s} \right)\)
Chọn D
Do vật di chuyển theo đường cong nên ta áp dụng công thức bổ đề tính công
Với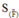
chính là độ dài đại số hình chiếu của đường cong lên phương của lực F