Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
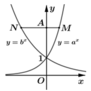
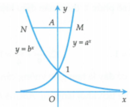
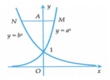
Gọi A(0;t) với t > 0. Suy ra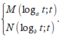 
Theo giả thiết AN = 2AM nên suy ra
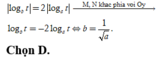
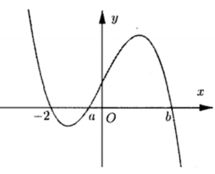
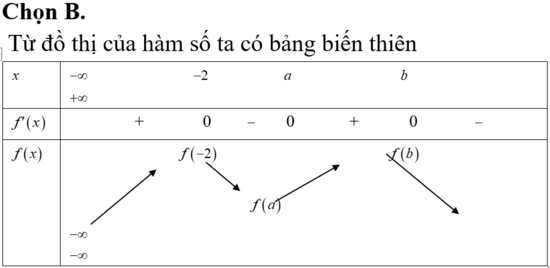
Đáp án B.
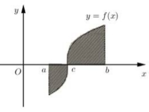
Phương pháp : Ứng dụng tích phân để tính diện tích hình phẳng.
Cách giải:
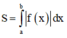
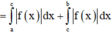
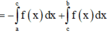
Đáp án A
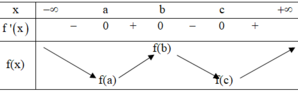
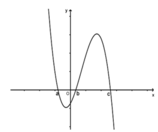
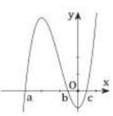
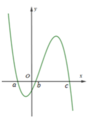
Dựa vào đồ thị của hàm số y = f '(x), em suy ra được bảng biến thiên như sau:
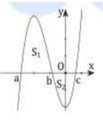
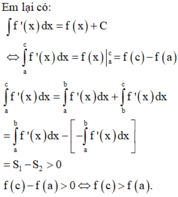
Đáp án C
Phương pháp:
+) 
đồng biến trên (a;b)
+) 
nghịch biến trên (a;b)
Cách giải:
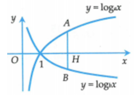
Quan sát đồ thị của hàm số y = f’(x), ta thấy:
+) 
đồng biến trên (a;b) => f(a) > f(b)
+) 
nghịch biến trên (b;c) => f(b)<f(c)
Như vậy, f(a)>f(b), f(c)>f(b)
Đối chiếu với 4 phương án, ta thấy chỉ có phương án C thỏa mãn
Đáp án C
Dựa vào đáp án, ta thấy rằng
(1) Đường thẳng f x = 0 ⇔ 3 2 x - 2 . 3 x = 0 ⇔ 3 x = 2 ⇔ x = log 3 2 ⇒ 1 đúng.
(2) Bất phương trình f x ≥ - 1 ⇔ 3 2 x - 2 . 3 x + 1 ≥ 0 ⇔ 3 x - 1 2 ≥ 0 , ∀ x ∈ ℝ . Nên f x ≥ - 1 có vô số nghiệm ⇒ 2 sai.
(3) Bất phương trình f x ≥ 0 ⇔ 3 x 2 - 2 . 3 x ≥ 0 ⇔ 3 x ≥ 2 ⇔ x ≥ log 3 2 ⇒ 3 sai.
(4) Đường thẳng f(x) = 0 chỉ có 1 nghiệm duy nhất ⇒ 4 sai
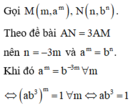
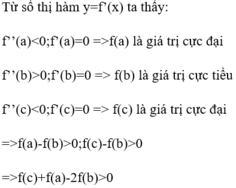
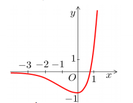
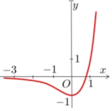
x A = - 1 ⇒ y = - 3 ⇒ A - 1 ; - 3 x B = 0 ⇒ y B = 11 ⇒ B 0 ; 1
Vì đường thẳng y = 1 - 2 x 1 + 2 x đi qua hai điểm A và B nên ta có hệ:
a - 1 + b = - 3 a . 0 + b = 1 ⇔ a = 4 b = 1
Vậy a b = 4
Đáp án B