K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

KN
15 tháng 7 2023
\(\widehat{xOy}+\widehat{x'Oy=180^0}\) (Vì \(\widehat{xOy}\) và \(\widehat{x'Oy}\) là hai góc kề bù)
\(\widehat{xOy}-\widehat{x'Oy}=40^0\)
a.\(\widehat{xOy}=\left(180^0+40^0\right):2=110^0\)
\(\widehat{x'Oy'}=\widehat{xOy}=110^0\) ( 2 góc đối đỉnh)
b. \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-110^0=70^0\) (2 góc kề bù)
\(\widehat{xOy'}=\widehat{x'Oy}=70^0\) ( 2 góc đối đỉnh)
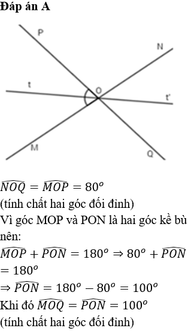
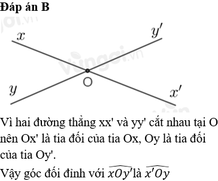
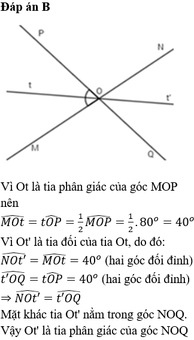
Vì góc x'Oy đối đỉnh xOy' cho nên xOy' = x'Oy = 60 độ nha
Đáp án : D
k mình nha
Tl
D nha