Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M E N F P D
Gọi AD là phân giác trong của \(\Delta\)ABC. Kéo dài DM cắt BE và CA lần lượt tại N và F, AN cắt BC tại P.
Dễ thấy \(\Delta\)ADB cân tại D có trung tuyến DM, suy ra DM là trung trực của AB
Do vậy ^DAN = ^DBN = 90o suy ra AP vuông góc AD hay AP là phân giác ngoài của \(\Delta\)ABC
Từ đó \(\left(BCPD\right)=-1\). Áp dụng phép chiếu xuyên tâm N: \(\left(BCPD\right)\rightarrow\left(ECFA\right)\)
Khi đó (ECFA) là hàng điều hòa. Mà ^AMF = 90o nên MA chính là phân giác của ^CME (đpcm).

Chỉ lm bài thoii, hình bn tự vẽ nha !!!
\(a.\) Tứ giác \(BEDC\) có \(\widehat{BEC}=\widehat{BDC}=90^0\)
Suy ra tứ giác \(BEDC\) là tứ giác nội tiếp
Tam giác \(DBA\) vuông tại \(D\) có đường cao \(DL\) nên suy ra \(BD^2=BL.BA\)
\(b.\) Tứ giác \(ADEH\) có:
\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\) nên tứ giác \(ADEH\) nội tiếp
Từ đó \(\widehat{BAK}=\widehat{BDE}\)
Mà \(\widehat{BJK}=\widehat{BAK}\) ( 2 góc nội tiếp cùng chắn một cung )
Do đó \(\widehat{BJK}=\widehat{BDE}\)

Ta có: Chiều cao của tháp DC = DC1 + C1C = 1,3 + DC1
=> DC = 1,3 + 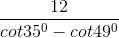
=> DC ≈ 22,8m
cãi đi bé Bài 11 trang 60 sgk hình học 10 - loigiaihay.com

a: Vì góc xOt>góc xOy
nên tia Ot không nằm giữa hai tia Ox và Oy
b: Vì góc tOx<góc tOy
nên tia Ot không nằm giữa hai tia Ox và Oy
c: Vì góc xOt=góc tOy
nên tia Ot nằm giữa hai tia Ox và Oy

Áp dụng định lý hàm sin cho tam giác BCD:
\(\frac{CD}{sin30^0}=\frac{BD}{sinC}=\frac{BD}{\frac{AB}{AC}}\Rightarrow AC.BD=2\)
Ta có: \(cosA=\frac{AB}{AC}=\frac{1}{AC}\)
Mà \(\frac{BD}{sinA}=\frac{AD}{sin60^0}\Rightarrow\frac{BD^2}{sin^2A}=\frac{AD^2}{sin^260}\Rightarrow\frac{4}{AC^2.\left(1-cos^2A\right)}=\frac{4\left(AC-1\right)^2}{3}\)
\(\Leftrightarrow\frac{1}{AC^2\left(1-\frac{1}{AC^2}\right)}=\frac{\left(AC-1\right)^2}{3}\) \(\Leftrightarrow\frac{1}{AC^2-1}=\frac{\left(AC-1\right)^2}{3}\)
\(\Leftrightarrow\left(AC^2-1\right)\left(AC-1\right)^2=3\)
\(\Leftrightarrow AC^4-2AC^3+2AC-4=0\)
\(\Leftrightarrow AC^3\left(AC-2\right)+2\left(AC-2\right)=0\)
\(\Leftrightarrow\left(AC^3+2\right)\left(AC-2\right)=0\Rightarrow AC=2\)