Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi chiều dài là x(m)(x>0)
thì chiều rộng : x-1(m)
vì độ dài mỗi đường chéo Của hình chữ nhật đó là 5m
=>pt: x^2+(x-1)^2=5^2
<=>x^2+x^2-2x+1-25=0
<=>2x^2-2x-24=0=>\(\Delta=\left(-2\right)^2-4\left(-24\right)2=196>0\)
=>\(\left\{{}\begin{matrix}x1=\dfrac{2+\sqrt{196}}{2.2}=4\left(TM\right)\\x2=\dfrac{2-\sqrt{196}}{2.2}=-3\left(loai\right)\end{matrix}\right.\)=> chiều dài là 4m , chiều rộng 3m
- Gọi các cạnh của HCN là a,b. Chu vi HCN là: \(2\left(a+b\right)=34\)nên \(a+b=17\)hay \(a=17-b\)
- Đường chéo của HCN là 13 nên theo định lý Pitago ta có: \(a^2+b^2=13^2\). Thay \(a=17-b\)
\(\left(17-b\right)^2+b^2=169\Leftrightarrow17^2-2\cdot17\cdot b+b^2+b^2=169\Leftrightarrow2b^2-34b+120=0\)
\(\Leftrightarrow b^2-17b+60=0\Leftrightarrow\left(b-5\right)\left(b-12\right)=0\Leftrightarrow\hept{\begin{cases}b=5\\b=12\end{cases}}\)
- Nếu b = 5 cm thì a = 17-5 = 12 cm.
- Nếu b = 12 cm thì a = 17-12 = 5 cm.

Bạn ơi Hình chũ nhật không có đường chéo
Chỉ có hình thoi mới có đường chéo thôi
HỌC TỐT !

Câu 1:
Gọi x là chiều dài mảnh đất (0<x<14; x>y)
Gọi y là chiều rộng mảnh vườn (0<y<14)
Vì chu vi mảnh đất bằng 20m nên ta có PT: x+y=14 (1)
Vì đường chéo mảnh đất bằng 10m nên ta có PT:
x2+y2=100 (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}x+y=14\\x^2+y^2=100\end{matrix}\right.\)(HPT dễ rồi bạn tự giải nha)
⇔\(\left\{{}\begin{matrix}y=8\\y=6\end{matrix}\right.\)(TM)
Vậy ta có 2 tập nghiệm (x;y) là (6;8) và (8;6)
-Độ dài 2 cạnh mảnh đất lần lượt là: 6cm và 8cm
Câu 1:
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của mảnh đất(Điều kiện: a>0; b>0 và \(a\ge b\))
Vì chu vi mảnh đất là 28m nên ta có phương trình:
2(a+b)=28
hay a+b=14(1)
Vì đường chéo hình chữ nhật là 10m nên Áp dụng định lí Pytago, ta được:
\(a^2+b^2=100\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=14\\a^2+b^2=100\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\\left(14-b\right)^2+b^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\b^2-28b+196+b^2-100=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\2b^2-28b+96=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\b^2-14b+48=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\\left(b-6\right)\left(b-8\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=14-8=6\\b=14-6=8\end{matrix}\right.\\\left[{}\begin{matrix}b=6\\b=8\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=8\\b=6\end{matrix}\right.\)(thỏa ĐK)
Vậy: Độ dài hai cạnh của mảnh đất hình chữ nhật lần lượt là 8m và 6m

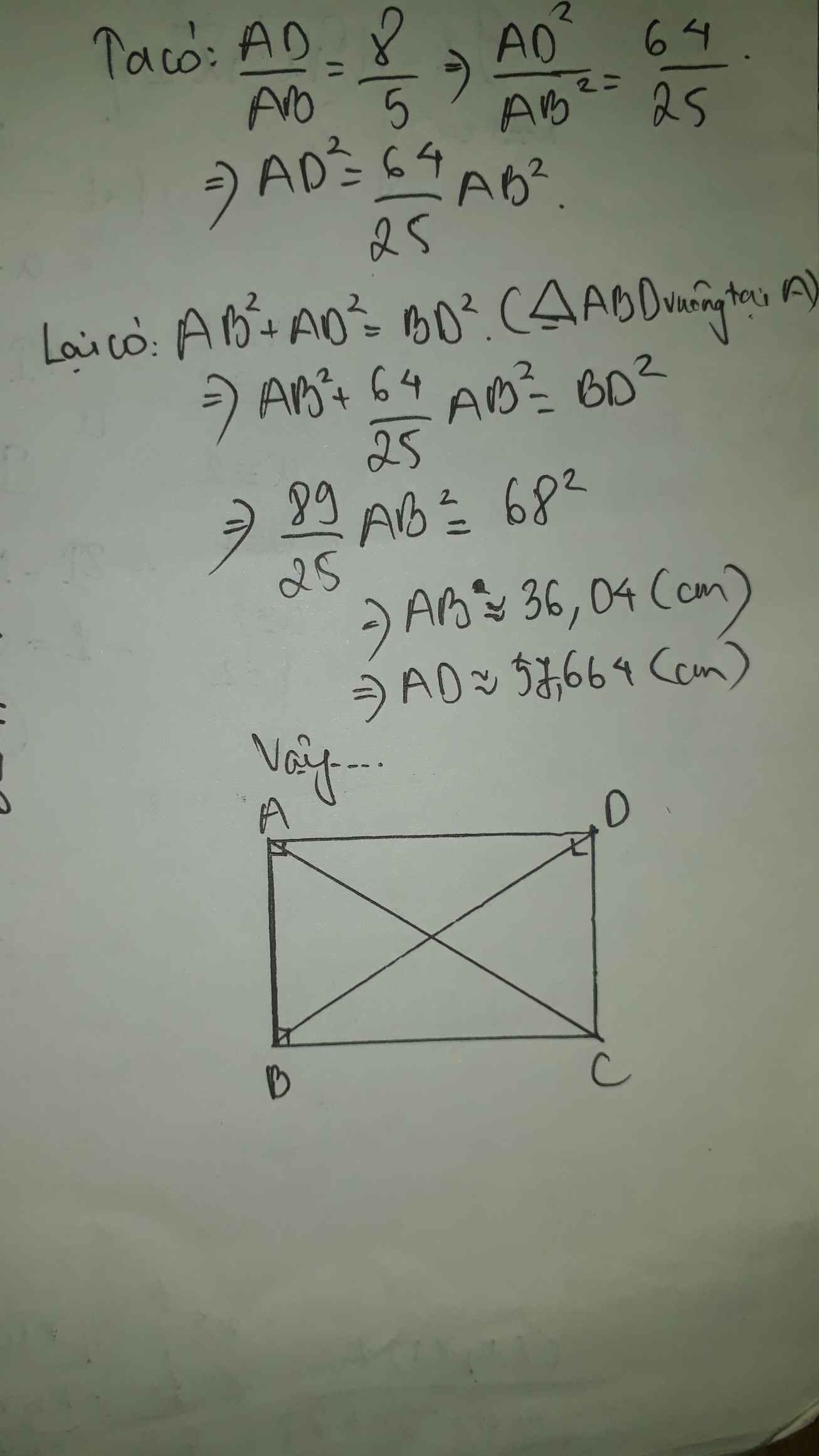
Ta có: \(\dfrac{AD}{AB}=\dfrac{8}{15}\)
nên \(AD=\dfrac{8}{15}AB\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow\left(\dfrac{8}{15}AB\right)^2+AB^2=68^2=4624\)
\(\Leftrightarrow AB^2\cdot\dfrac{289}{225}=4624\)
\(\Leftrightarrow AB^2=3600\)
\(\Leftrightarrow AB=60\left(cm\right)\)
\(\Leftrightarrow AD=\dfrac{8}{15}AB=\dfrac{8}{15}\cdot60=32\left(cm\right)\)
\(\Leftrightarrow CD=60cm;BC=32cm\)

Gọi chiều dài của hcn là a, chiều rộng của hcn là b
(cm; a>b>0)
Ta có: a2 + b2 = 292 (Pytago)
<=> a2 + b2 = 841
TH1: a = 20
<=> 202 + b2 = 841
<=> b = 21 (loại)
TH2: b = 20
<=> a2 + 202 = 841
<=> a = 21 (t/m)
=> Chiều dài hcn là 21cm, chiều rộng hcn là 20cm