Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
Sử dụng phương pháp dựng tam giác vuông đã được học.
Học sinh tự vẽ hình
Ta lần lượt thực hiên:
- Vẽ đoạn BC = 4cm.
- Vẽ tia Bx tạo với BC một góc 650
- Vẽ đường thẳng a qua C và vuông góc với Bx và cắt Bx tại A.
Khi đó ∆ABC là tam giác cần dựng.

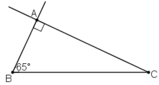
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.

Bạn tự vẽ hình nhé!
À mà mình chỉ giải cho bạn câu 1 và 2 thôi câu 3 mình đang suy nghĩ hình rối quá
1) Gọi AD và BE lần lượt là hai đường cao của \(\Delta\) ABC .
Theo đề hai đường cao AD và BE cắt nhau tại H hay H là trực tâm của \(\Delta\) ABC
=> CH là đường cao thứ 3 của \(\Delta\) ABC
=> CH \(\perp\) AB (1)
mà BD \(\perp\) AB (gt) => CH//BD
Có BH \(\perp\) AC (BE là đường cao)
CD \(\perp\) AC
=> BH//CD (2)
Từ (1) và (2) suy ra : Tứ giác BHCD là hình bình hành
2) Có BHCD là hình bình hành nên 2 đường chéo cắt nhau tại trung điểm mỗi đường mà M là trung điểm của BC => M cũng là trung điểm của HD hay HM = DM
Có O là trung điểm của AD hay OA = OD
Xét \(\Delta\) AHD có:
HM = DM
OA = OD
=> OM là đường trung bình của \(\Delta\) AHD
=> OM = \(\frac{1}{2}\) AH hay AH = 2 OM
XONG !!![]()

a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.