Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán

Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC

+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

Trình tự dựng gồm các bước sau:
- Dựng đoạn thẳng BC = 6cm
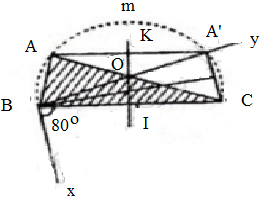
- Dựng cung chứa góc 80 trên đoạn thẳng BC (cung BmC).
- Trên đường vuông góc với BC tại I(I là trung điểm BC), chọn điểm K sao cho IK = 2cm. Từ K dựng đường thẳng vuông góc với IK. Đường thẳng này cắt cung chứa góc BmC tại A và A'.
ΔABC (hoặc ΔA'BC) là tam giác thỏa mãn yêu cầu đề bài.
Cho tam giác vuông ABC ( \(\widehat{A}=90^0\)) có đường cao AH = 6 cm , BC = 10 cm. Tính \(S_{ABC}\)

A B C H
\(S_{\Delta ABC}=\frac{AH\cdot BC}{2}=\frac{6\cdot10}{2}=\frac{60}{2}=30\left(cm^2\right)\)
Vậy \(S_{\Delta ABC}=30cm^2\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)

a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
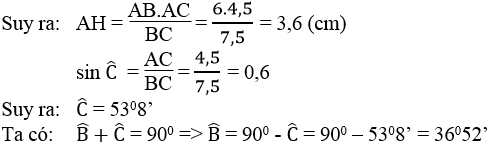 b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.

Ta có:\(sin\widehat{BAH}\)=\(\frac{2}{3}\)\(\Rightarrow sin\widehat{BAH}\)\(\approx sin42^o\)
\(\Rightarrow\widehat{BAH}\)=\(42^o\)
Vì AH là đường cao => \(AH\perp BC=\left\{H\right\}\)
\(\Rightarrow\widehat{AHB}\)=\(\widehat{AHC}\)=\(90^O\)
Xét tam giác AHB vuông tại H:
\(\widehat{BAH}\)+\(\widehat{B}\)=\(90^O\)\(\Rightarrow\widehat{B}\)=\(48^O\)
Xét tam giác ABC vuông tại A, đường cao AH:
+) \(sin\widehat{B}\)=\(\frac{AC}{BC}\)\(\Leftrightarrow sin48^o=\frac{3}{BC}\)
\(\Rightarrow BC=4\left(cm\right)\)
+) \(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}\)
\(\Rightarrow AB\approx2,6\left(cm\right)\)
+) \(AH.BC=AB.AC\)(hệ thức giữa cạnh và đường cao)
\(\Rightarrow AH=\frac{AB.AC}{BC}\)
\(\Rightarrow AH\approx2\left(cm\right)\)
\(S\)ABC =\(\frac{AH.BC}{2}\)= \(4\left(cm^2\right)\)
*Mình sợ sẽ có sai sót nên bạn kiểm tra lại nhé
~HỌC TỐT~

Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là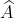 ,
, 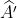 . Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là \(\widehat{A}\) , \(\widehat{A'}\). Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán