Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\left\{{}\begin{matrix}x>2\\\frac{5}{2}+3\le x+\frac{3}{2}x\\2x\le5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>2\\\frac{5}{2}x\ge\frac{11}{2}\\x\le\frac{5}{2}\end{matrix}\right.\) \(\Rightarrow\frac{11}{5}\le x\le\frac{5}{2}\)
\(\Rightarrow a+b=\frac{11}{5}+\frac{5}{2}=D\)
2.
\(\left\{{}\begin{matrix}6x-4x>7-\frac{5}{7}\\4x-2x< 25-\frac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>\frac{22}{7}\\x< \frac{47}{4}\end{matrix}\right.\)
\(\Rightarrow\frac{22}{7}< x< \frac{47}{4}\Rightarrow x=\left\{4;5...;11\right\}\) có 8 giá trị
3.
\(\left\{{}\begin{matrix}5x-4x< 5+2\\x^2< x^2+4x+4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< 7\\x>-1\end{matrix}\right.\)
\(\Rightarrow-1< x< 7\Rightarrow x=\left\{0;1;...;6\right\}\)
\(\Rightarrow\sum x=1+2+...+6=21\)
4.
\(\left\{{}\begin{matrix}x^2-2x+1\le8-4x+x^2\\x^3+6x^2+12x+8< x^3+6x^2+13x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\le7\\x\ge-1\end{matrix}\right.\) \(\Rightarrow-1\le x\le\frac{7}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{min}=-1\\x_{max}=3\end{matrix}\right.\) \(\Rightarrow S=2\)
5.
\(\left\{{}\begin{matrix}x>\frac{1}{2}\\x< m+2\end{matrix}\right.\)
Hệ đã cho có nghiệm khi và chỉ khi:
\(m+2>\frac{1}{2}\Rightarrow m>-\frac{3}{2}\)

a)\(\left\{{}\begin{matrix}2m-1>0\Rightarrow m>\dfrac{1}{2}\left(1\right)\\m^2-\left(m-2\right)\left(2m-1\right)< 0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow m^2-\left(2m^2-m-4m+2\right)=-m^2+5m-2< 0\)
\(m^2-5m+2>0\Rightarrow\left[{}\begin{matrix}m< \dfrac{5-\sqrt{17}}{2}< \dfrac{1}{2}\\m>\dfrac{5+\sqrt{17}}{2}\end{matrix}\right.\)
Nghiệm hệ là
\(m>\dfrac{5+\sqrt{17}}{2}\)
b)\(\left\{{}\begin{matrix}m^2-m-2< 0\left(1\right)\\\left(2m-1\right)^2-4\left(m^2-m-2\right)\le0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\left(2m-1\right)^2-4\left(m^2-m-2\right)=9< 0,\forall m\).
Suy ra (2) vô nghiệm .
Kết luận hệ vô nghiệm.

a)
\(\left\{{}\begin{matrix}x^2\ge\dfrac{1}{4}\left(1\right)\\x^2-x\le0\left(2\right)\end{matrix}\right.\)
\(\left(1\right)x^2-0,25\Leftrightarrow\left[{}\begin{matrix}x\le-\dfrac{1}{2}\\x\ge\dfrac{1}{2}\end{matrix}\right.\)
(2)\(x^2-x\le\) \(\Leftrightarrow0\le x\le1\)
Kết hợp (1) và (2) \(\Rightarrow\dfrac{1}{2}\le x\le1\)
b)
\(\left\{{}\begin{matrix}\left(x-1\right)\left(2x+3\right)>0\left(1\right)\\\left(x-4\right)\left(x+\dfrac{1}{4}\right)\le0\left(2\right)\end{matrix}\right.\)
Giải: \(\left(1\right)\left(x-1\right)\left(2x+3\right)>0\Leftrightarrow\left[{}\begin{matrix}x< -\dfrac{3}{2}\\x>1\end{matrix}\right.\)
Giải: (2) \(\left(x-4\right)\left(x+\dfrac{1}{4}\right)< 0\Leftrightarrow-\dfrac{1}{4}\le x\le4\)
Kết hợp điều kiện của (1) và (2) ta có: (1;4] là nghiệm của hệ bất phương trình.

a)
\(\left\{{}\begin{matrix}x^2+x+5< 0\\x^2-6x+1>0\end{matrix}\right.\)
\(\)Ta có
\(x^2+x+5=\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{19}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}>0\)
=> Bất phương trình đàu tiên sai, hệ bất phương trình sai
b)
\(\left\{{}\begin{matrix}2x^2+x-6>0\\3x^2-10x+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)\left(x+2\right)>0\\\left(x-3\right)\left(3x-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\\\left[{}\begin{matrix}x\le-\dfrac{1}{3}\\x\ge3\end{matrix}\right.\end{matrix}\right.\)

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
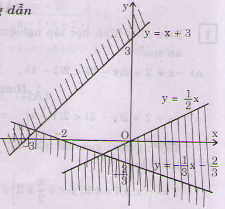
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
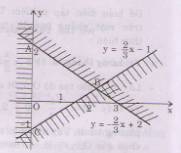

c)
\(\left\{\begin{matrix} -x^2+4x-7< 0\\ x^2-2x-1\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^2-4x+7>0\\ x^2-2x+1\geq 2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (x-2)^2+3>0\\ (x-1)^2-2\geq 0\end{matrix}\right.\Leftrightarrow (x-1)^2-2\geq 0\Leftrightarrow \left[\begin{matrix} x-1\geq \sqrt{2}\\ x-1\leq -\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} x\geq \sqrt{2}+1\\ x\leq 1-\sqrt{2}\end{matrix}\right.\)
d)
\(\left\{\begin{matrix} -2x^2-5x+4< 0\\ -x^2-3x+10>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x^2+5x-4>0\\ (2-x)(x+5)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2(x+\frac{5}{4})^2-\frac{57}{8}>0\\ (2-x)(x+5)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (x+\frac{5}{4}-\frac{\sqrt{57}}{4})(x+\frac{5}{4}+\frac{\sqrt{57}}{4})>0\\ (2-x)(x+5)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>\frac{-5+\sqrt{57}}{4}\\ x< \frac{-5-\sqrt{57}}{4}\end{matrix}\right.\\ -5< x< 2\end{matrix}\right.\) \(\Rightarrow \left[\begin{matrix} -5< x< \frac{-5-\sqrt{57}}{4}\\ \frac{\sqrt{57}-5}{4}< x< 2\end{matrix}\right.\)
a)
\(\left\{\begin{matrix} 2x^2+9x+7>0\\ x^2+x-6< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x+1)(2x+7)>0\\ (x-2)(x+3)< 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>-1\\ x< \frac{-7}{2}\end{matrix}\right.\\ -3< x< 2\end{matrix}\right.\Rightarrow -1< x< 2\)
b) \(\left\{\begin{matrix} 2x^2+x-6>0\\ 3x^2-10x+3\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (2x-3)(x+2)>0\\ (x-3)(3x-1)\geq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>\frac{3}{2}\\ x< -2\end{matrix}\right.\\ \left[\begin{matrix} x\geq 3\\ x\leq \frac{1}{3}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow \left[\begin{matrix} x\geq 3\\ x< -2\end{matrix}\right.\)

a)\(\left\{{}\begin{matrix}2x-3y=1\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot\left(3-2y\right)-3y=1\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6-7y=1\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{7}\\x=3-2\cdot\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{7}\\x=\dfrac{11}{7}\end{matrix}\right.\)b) Biểu diễn lại một biến theo một biến như pt trên rồi giải, ta có :
\(\left\{{}\begin{matrix}2x+4y=5\\4x-2y=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{9}{10}\\y=\dfrac{4}{5}\end{matrix}\right.\)
c) Cách làm tương tự như pt a ta có :
\(\left\{{}\begin{matrix}\dfrac{2}{3}x+\dfrac{1}{2}y=\dfrac{2}{3}\\\dfrac{1}{3}x-\dfrac{3}{4}y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{9}{8}\\y=-\dfrac{1}{6}\end{matrix}\right.\)
d) Tương tự ta có :
\(\left\{{}\begin{matrix}0,3x-0,2y=0,5\\0,5x+0,4y=1,2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
Lời giải:
Giả sử cả 2 pt trên đều không có nghiệm.
Khi đó:
\(\left\{\begin{matrix} \Delta_1=a^2-4b< 0\\ \Delta_2=c^2-4d< 0\end{matrix}\right.\)
\(\Rightarrow a^2+c^2< 4(b+d)\)
Kết hợp với đk: \(ac\geq 2(b+d)\Rightarrow 2ac> a^2+c^2\)
\(\Leftrightarrow a^2+c^2-2ca< 0\Leftrightarrow (a-c)^2< 0\) (vô lý)
Do đó điều giả sử là sai.
Tức là ít nhất 1 trong 2 pt trên phải có nghiệm.