Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

|
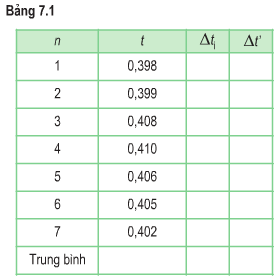
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |


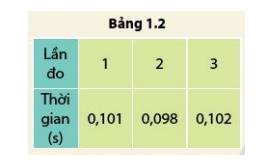
Thời gian trung bình của phép đo là:
\(\overline t = \frac{{{t_1} + {t_2} + {t_3}}}{3} = \frac{{0,101 + 0,098 + 0,102}}{3} \approx 0,100(s)\)
Sai số tuyệt đối trung bình của phép đo là:
\(\begin{array}{l}\Delta {t_1} = \left| {{t_2} - {t_1}} \right| = \left| {0,098 - 0,101} \right| = 0,003\\\Delta {t_2} = \left| {{t_3} - {t_2}} \right| = \left| {0,102 - 0,098} \right| = 0,004\\\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2}}}{2} = \frac{{0,003 + 0,004}}{2} \approx 0,004(s)\end{array}\)

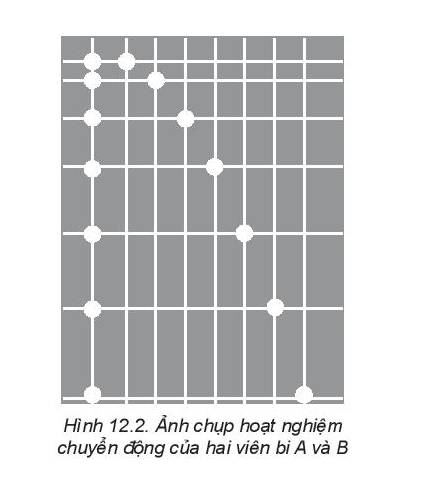
Thông qua quan sát, ta thấy tọa độ tính theo phương ngang của hai viên bi A và viên bi B đều không thay đổi, và đều trong cùng một khoảng thời gian
Mặt khác, ta có \(v=\dfrac{s}{t}=\dfrac{x}{t}\)
(do vật không đổi chiều chuyển động). Tọa độ x không đổi, thời gian như nhau, nên vận tốc không thay đổi
\(\Rightarrow v_x=v_0\)
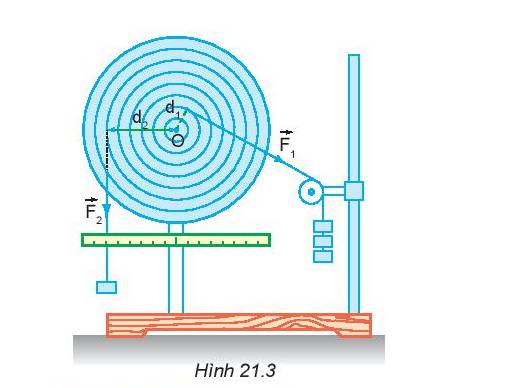
1.
Nếu bỏ lực \(\overrightarrow {{F_1}} \) thì đĩa quay ngược chiều kim đồng hồ.
2.
Nếu bỏ lực \(\overrightarrow {{F_2}} \) thì đĩa quay theo chiều kim đồng hồ

Các em thực hành theo hướng dẫn của giáo viên.
Ví dụ cho kết quả thí nghiệm
Bảng 6.1
Quãng đường: s = 0,5 (m)

- Tốc độ trung bình: \(\overline v = \frac{s}{{\overline t }} = \frac{{0,5}}{{0,778}} = 0,643(m/s)\)
- Sai số:
\(\begin{array}{l}\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + ... + \Delta {t_n}}}{n} = \frac{{0,001 + 0,002 + 0,002}}{3} \approx 0,002(s)\\\delta t = \frac{{\overline {\Delta t} }}{{\overline t }}.100\% = \frac{{0,002}}{{0,778}}.100\% = 0,3\% \\\delta s = \frac{{\overline {\Delta s} }}{s}.100\% = \frac{{0,0005}}{{0,5}}.100\% = 0,1\% \\\delta v = \delta s + \delta t = 0,1\% + 0,3\% = 0,4\% \\\Delta v = \delta v.\overline v = 0,4\% .0,643 = 0,003\\ \Rightarrow v = 0,643 \pm 0,003(m/s)\end{array}\)
Bảng 6.2
Đường kính của viên bi: d = 0,02 (m); sai số: 0,02 mm = 0,00002 (m)

- Tốc độ tức thời: \(\overline v = \frac{d}{{\overline t }} = \frac{{0,02}}{{0,032}} = 0,625(m/s)\)
- Sai số:
\(\begin{array}{l}\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + ... + \Delta {t_n}}}{n} = \frac{{0,001 + 0 + 0,00}}{3} \approx 0,001(s)\\\delta t = \frac{{\overline {\Delta t} }}{{\overline t }}.100\% = \frac{{0,001}}{{0,032}}.100\% = 2,1\% \\\delta s = \frac{{\overline {\Delta s} }}{s}.100\% = \frac{{0,00002}}{{0,02}}.100\% = 0,1\% \\\delta v = \delta s + \delta t = 0,1\% + 2,1\% = 2,2\% \\\Delta v = \delta v.\overline v = 2,2\% .0,0032 = 0,001\\ \Rightarrow v = 0,625 \pm 0,014(m/s)\end{array}\)
Nhận xét: Tốc độ trung bình gần bằng tốc độ tức thời, vì viên bi gần như chuyển động đều.
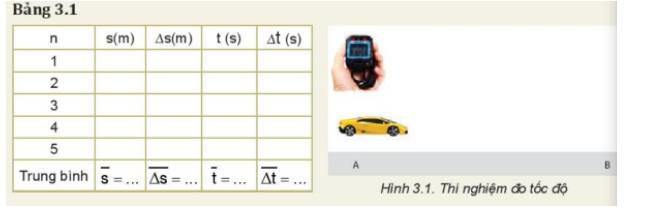



a) Nguyên nhân gây ra sự sai khác giữa các lần đo là:
- Do đặc điểm và cấu tạo của dụng cụ đo
- Do điều kiện làm thí nghiệm chưa được chuẩn
- Do thao tác khi đo
b) Ta có:
\(\overline {\Delta s} = \frac{{\left| {\overline s - {s_1}} \right| + \left| {\overline s - {s_2}} \right| + ... + \left| {\overline s - {s_5}} \right|}}{5} = 0,00168\)
\(\overline {\Delta t} = \frac{{\left| {\overline t - {t_1}} \right| + \left| {\overline t - {t_2}} \right| + ... + \left| {\overline t - {t_5}} \right|}}{5} = 0,0168\)
c) Viết kết quả đo:
Ta có:
\(\Delta s = \overline {\Delta s} + \Delta {s_{dc}} = 0,00168 + \frac{{0,001}}{2} = 0,00218\)
\(\Delta t = \overline {\Delta t} + \Delta {t_{dc}} = 0,0168 + \frac{{0,01}}{2} = 0,0218\)
Suy ra:
\(s = \overline s \pm \Delta s = 0,6514 \pm 0,00218\left( m \right)\)
\(t = \overline t \pm \Delta t = 3,514 \pm 0,0218\left( s \right)\)
d) Tính sai số tỉ đối:
\(\delta t = \frac{{\Delta t}}{{\overline t }}.100\% = \frac{{0,0218}}{{3,514}}.100\% = 0,620\)
\(\delta s = \frac{{\Delta s}}{{\overline s }}.100\% = \frac{{0,00218}}{{0,6514}}.100\% = 0,335\)
\(\delta v = \frac{{\Delta s}}{{\overline s }}.100\% + \frac{{\Delta t}}{{\overline t }}.100\% = 0,335 + 0,620 = 0,955\)
\(\Delta v = \delta v.\overline v = 0,955.\frac{{0,6514}}{{3,514}} = 0,177\left( {m/s} \right)\)