

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



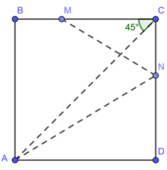
Phân tích: Vì ABCD là hình vuông nên:
Ta có, ba điểm A, M, N cố định nên bài toán quy về việc dựng đỉnh C. Đỉnh C là giao điểm của :
- Cung chứa góc 90 ° dựng trên đoạn thẳng MN
- Cung chứa góc 45 ° dựng trên đoạn thẳng AM
Cách dựng:
- Dựng cung chứa góc 90 ° trên đoạn MN
- Dựng cung chứa góc 45 ° trên đoạn AM
Hai cung cắt nhau tại C
- Nối CM ,CN
- kẻ AB ⊥ CM tại B , AD ⊥ CN tại D
Tứ giác ABCD là hình vuông cần dựng

Tam giác L BCM = tam giác L CDN (2 cạnh góc L = nhau)
=> CDN^ = BCM^
lại có:
BMC^ = DCI^ (so le trong)
=> CID^ =CBM^ = 1v (xét 2 tam giác CDI và CBM)
gọi P là trung điểm của CD và Q là giao điểm của AP và DN
ta có tứ giác AMCP là hình bình hành vì có AM//=CP
=> AP // CM
=> AP L DN
xét tam giác DCI có P là trung điểm của CD và PQ // CI nên Q là trung điểm của DI
vậy AQ là đường cao vùa là trung tuyến của tam giác ADI => tam giác ADI cân tại A => AD=AI
~~~~~~~~~~~~~~~~~~~~ ai đi qua nhớ để lại ~~~~~~~~~~~~~~~~~~
Kéo dài BO cắt AC tại H.Nhận thấy O là trọng tâm tam giác ABC>>>BO=2/3BH.Mà BH dễ tính do tam giác ABC vuông cân.
>>>Tính được BO(nhớ k nha)

Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [B, A] Đoạn thẳng i: Đoạn thẳng [C, A] Đoạn thẳng q: Đoạn thẳng [B, H] Đoạn thẳng r: Đoạn thẳng [D, E] Đoạn thẳng s: Đoạn thẳng [H, E] Đoạn thẳng t: Đoạn thẳng [F, G] Đoạn thẳng a: Đoạn thẳng [F, K] Đoạn thẳng b: Đoạn thẳng [A, F] Đoạn thẳng c: Đoạn thẳng [K, C] Đoạn thẳng d: Đoạn thẳng [H, K] Đoạn thẳng e: Đoạn thẳng [H, D] Đoạn thẳng f_1: Đoạn thẳng [K, D] Đoạn thẳng g_1: Đoạn thẳng [I, J] B = (-0.92, 2.22) B = (-0.92, 2.22) B = (-0.92, 2.22) C = (7.22, 2.18) C = (7.22, 2.18) C = (7.22, 2.18) Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm D: Điểm trên f Điểm D: Điểm trên f Điểm D: Điểm trên f Điểm F: Giao điểm đường của j, k Điểm F: Giao điểm đường của j, k Điểm F: Giao điểm đường của j, k Điểm E: Giao điểm đường của j, h Điểm E: Giao điểm đường của j, h Điểm E: Giao điểm đường của j, h Điểm H: Giao điểm đường của l, m Điểm H: Giao điểm đường của l, m Điểm H: Giao điểm đường của l, m Điểm K: Giao điểm đường của n, p Điểm K: Giao điểm đường của n, p Điểm K: Giao điểm đường của n, p Điểm I: Giao điểm đường của h, e Điểm I: Giao điểm đường của h, e Điểm I: Giao điểm đường của h, e Điểm J: Giao điểm đường của i, f_1 Điểm J: Giao điểm đường của i, f_1 Điểm J: Giao điểm đường của i, f_1 Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1
a) Ta thấy \(\widehat{BDI}=\widehat{BCA}\left(=\widehat{IBD}\right)\), suy ra ID // AJ
Tương tự DJ // IA. Vậy tứ giác AIDJ là hình bình hành hay AJ song song và bằng ID.
Từ đó suy ra AJ cũng song song và bằng HI hay AHIJ là hình bình hành. Vậy thì HA // IJ (1)
Xét tam giác HDK có IJ là đường trung bình nên HK // IJ (2)
Từ (1) và (2) suy ra H, A, K thẳng hàng.
b) Ta thấy do AHIJ là hình bình hành nên IJ = AH. Lại có \(IJ=\frac{HK}{2}\Rightarrow HA=\frac{HK}{2}\)
Vậy A là trung điểm của HK.
c) Do AIDJ là hình bình hành nên trung điểm IJ cũng là trung điểm AD.
Vậy khi D thay đổi, M luôn là trung điểm AD. Nói cách khác, khi M thay đổi M sẽ di chuyển trên đường trung bình ứng với đáy BC của tam giác ABC.

Câu hỏi của Hai Nguyen Lam - Toán lớp 9 - Học toán với OnlineMath Bạn tham khảo bài làm ở link này nhé!

A B C D F E M
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)