Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy, khi vẽ hình như trên, ta đã vẽ 2 góc A và B có số đo bằng nhau (đều bằng \(60^\circ \)).
Mà 2 góc này ở vị trí đồng vị
Vậy a//b (Dấu hiệu nhận biết 2 đường thẳng song song)

a
) x O y M A B d
b
A O B m C n D M
c
A B C d 1 2 d D
d
A B C
ĐÃ VẼ LẠI 2 LẦN.LẦN NÀY LÀ LẦN 3
=> CUỘC ĐỜI ĐEN NHỌ CỦA COOL KID :V

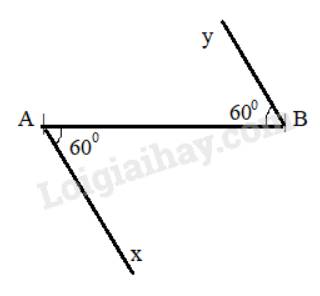
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).

Trong sách có đó, vào đó mừ xem, ko hiểu j hỏi mình
Nếu ko dùng ê ke thì dúng thước đo độ cx đc
Cách làm:
Vẽ đường thẳng đi qua điểm A sao cho có số đo theo yêu cầu
Vẽ tiếp đg thẳng b đi qua đg thẳng A sao cho có số đo = vs số đo nêu trên
=> Có đc 2 đg thẳng song song
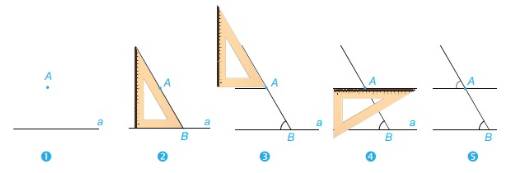
+ Dùng góc vuông:
Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
Bước 2: Đặt ê ke sao cho 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, 1 cạnh góc vuông còn lại đi qua điểm A, ta kẻ đường thẳng b đi qua A, vuông góc với a.
Bước 3: Kẻ đường thẳng đi qua A, vuông góc với đường thẳng b.
Ta được đường thẳng b đi qua A và song song với a.
+ Dùng góc 30\(^\circ \)của êke:
Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
Bước 2: Đặt ê ke sao cho góc nhọn 30\(^\circ \) và 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, cạnh đối diện với góc vuông đi qua điểm A, ta kẻ đường thẳng c đi qua cạnh đối diện với góc vuông của ê ke.
Bước 3: Dịch chuyển ê ke theo đường thẳng c cho đến khi điểm A trùng với đỉnh của góc nhọn 30\(^\circ \).
Bước 4: Kẻ đường thẳng b đi qua A và 1 cạnh của góc 30\(^\circ \)
Ta được đường thẳng b đi qua A và song song với a.