Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
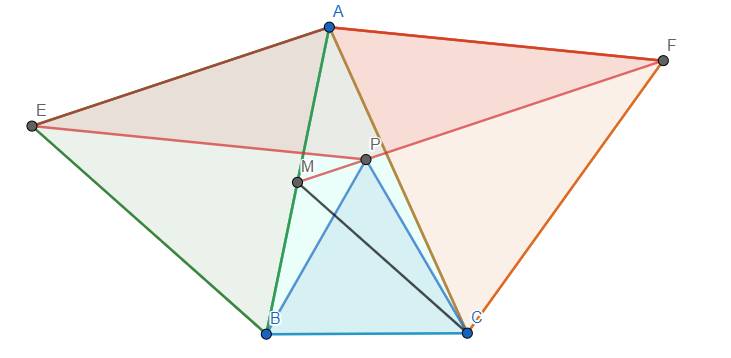
Gọi M là giao điểm của PE với AB.
Ta thấy rằng \(CF=AF=PE,PF=AE=EB\)
Đồng thời \(\widehat{BEP}=60^o-\widehat{AEP}=60^o-\widehat{AFP}=\widehat{PFC}\)
Dẫn đến \(\Delta PBE=\Delta CPF\left(c.g.c\right)\)
\(\Rightarrow PB=PC\) (1)
Mặt khác, \(\widehat{AMF}=\widehat{MAE}=60^o=\widehat{ACF}\) nên tứ giác AMCF nội tiếp.
\(\Rightarrow\widehat{BAC}=\widehat{PFC}\). Mà lại có \(AB=PF,AC=FC\) nên suy ra \(\Delta ABC=\Delta FPC\left(c.g.c\right)\)
\(\Rightarrow PC=BC\) (2)
Từ (1) và (2) \(\Rightarrow\Delta PBC\) đều (đpcm)
Trên nửa mặt phẳng bờ là NF, dựng tam giác đều NFG. Nối G với A và H.
Ta có: ^CFN + ^AFN = 600; ^AFG + ^AFN = 600 => ^CFN = ^AFG.
Xét \(\Delta\)NFC và \(\Delta\)GFA có: FC=FA; ^CFN=^AFG; FN=FG => \(\Delta\)NFC = \(\Delta\)GFA (c.g.c)
=> CN=AG (2 cạnh tương ứng) . Mà CN=BN nên BN=AG.
Lại có: \(\Delta\)ABE là tam giác đều với trực tâm H => ^ABH=300
=> ^HBN = ^ABC + ^ABH = ^ABC +300 (1)
^HAG = 3600 - (^FAG + ^FAC + ^BAC + ^HAB) (*)
Do \(\Delta\)NFC=\(\Delta\)GFA => ^FAG = ^FCN (2 góc tương ứng) => ^FAG = ^ACB +600
Dễ thấy: \(\Delta\)ACF đều => ^FAC = 600; \(\Delta\)ABE đều, trực tâm H => ^HAB = ^ABH = 300
Thay hết vào (*), ta được: ^HAG = 3600 - (^ACB + 600 + 600 + ^BAC + 300)
=> ^HAG = 2100 - (^BAC + ^ACB) = 1800 - (^BAC + ^ACB) +300 = ^ABC + 300
=> ^HAG = ^ABC + 300 (2)
Từ (1) và (2) => ^HBN = ^HAG.
Xét \(\Delta\)BHN và \(\Delta\)AHG có: BH=AH (Dễ c/m); ^HBN = ^HAG; BN=AG (cmt)
=> \(\Delta\)BHN=\(\Delta\)AHG (c.g.c) => HN=HG (2 cạnh tương ứng).
Xét \(\Delta\)HNF và \(\Delta\)HGF: GN=HG; FN=FG; HF chung => \(\Delta\)HNF=\(\Delta\)HGF (c.c.c)
=> ^HFG = ^HFN = ^GFN/2 = 600/2 = 300; ^NHF = ^GHF
\(\Delta\)BHN=\(\Delta\)AHG => ^BHN = ^AHG . Mà ^BHN + ^NHA = ^BHA = 1200
=> ^AHG + ^NHA = ^NHG = 1200 => ^NHF = ^GHF = ^NHG/2 = 600
Vậy \(\Delta\)FNH có: ^HFN = 300; ^NHF = 600 => ^FNH = 900.
Còn 1 cách khác ở trong sách Nâng cao phát triển Toán 7 - T2 nhé!
Mình nghĩ thêm cách này để bạn tham khảo ^-^
Cho cái link này không bít có đúng không:
https://cunghoctot.vn/forum/topic/1003161
Chia ra 3 trường hợp .....
Sửa đề: Đa giác đều 15 cạnh
=>Tạo ra 3 ngũ giác đều trong đó: Ngũ giác 1 có các đỉnh tô màu đỏ, ngũ giác 2 có các đỉnh tô màu xanh, ngũ giác 3 có các đỉnh tô màu vàng. Ta sẽ xem 3 ngũ giác đó như là 3 khu, 7 điểm ta chọn ra 7 điểm trong đó.
=>7 điểm thuộc vào 3 khu khác nhau thì phải có 1 khu có 3 điểm.
=>Luôn có tam giác cân(3 đỉnh bất kì của một ngũ giác đều tạo thành tam giác cân)
ΔABC đều ⇒\(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
\(\widehat{B}=\widehat{EMF}=60^o\) mà 2 góc này là 2 góc SLT ⇒AB//FM⇒AE//FM (1)
\(\widehat{C}=\widehat{EMF}=60^o\)mà 2 góc này là 2 góc SLT ⇒AC//EM⇒AF//EM (2)
Từ (1) và (2) ⇒ AEMF là hbh
\(\Rightarrow\widehat{AEM}=\widehat{AFM}\Rightarrow\widehat{BEM}=\widehat{CFM}\) (kề bù với 2 góc bằng nhau)
Xét Δ BEM và ΔCMF có:
\(\widehat{B}=\widehat{C}\left(=60^o\right)\)
\(\widehat{BEM}=\widehat{CFM}\) (chứng minh trên)\
⇒Δ BEM ∼ ΔCMF(g.g)
