Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
T 2 = T 1 + 80 ; p 2 = p 1 + 25 100 . p 1 = 1 , 25 p 1
Áp dụng công thức quá trình đẳng nhiệt
p 1 T 1 = p 2 T 2 ⇒ T 1 = T 2 . p 1 p 2 = ( T 1 + 80 ) . p 1 1 , 25 p 1 = T 1 + 80 1 , 25 ⇒ T 1 = 320 K
Mà T 1 = 273 + t ⇒ t = 47 0 C

a) Tính nhiệt độ ban đầu của khí.
Trong biến đổi đẳng áp, công của khí :
\(A'p\Delta V=\frac{m}{\mu}R\Delta T\Rightarrow\Delta T\frac{\mu\Delta'}{mR}=300K\)
Biến đổi đẳng áp : \(\frac{T_2}{T_1}=\frac{V_2}{V_1}=2\Rightarrow T_2=2T_1\)
\(\Delta T=T_2-T_1=T_1=300K\Rightarrow t_1=27^oC\)
b) Tính nhiệt lượng.
Biến đổi đẳng áp :\(Q=mc_p\Delta T=55200\left(J\right)\)
Tính \(\Delta U\)
c)Độ biến thiên nội năng của khí :
\(\Delta u=Q+A=Q-A'=39628\left(J\right)\)


Khi pit tông đứng yên (trước và sau khi di chuyển) nến áp suất của khí hai bên pti tông là như nhau.
Áp dụng phương trình trạng thái cho khí trong mỗi phần xilanh :
- Phần khí bị nung nóng : $\dfrac{p_0V_0}{T_0}=\dfrac{p_1V_1}{T_1} (1) $
- Phần khí bị làm lạnh : $\dfrac{p_0V_0}{T_0}=\dfrac{p_2V_2}{T_2} (2) $
Từ phương trình $(1),(2)$ và $p_1=p_2\Rightarrow \dfrac{V_1}{T_1}=\dfrac{V_2}{T_2} $
Gọi x là khoảng pit tông dịch chuyển ta có :$\dfrac{(l_0+x)S}{T_1}=\dfrac{(l_0-x)S}{T_2}\Rightarrow x=\dfrac{l_0(T_1-T_2)}{T_1+T_2} $
Thay số ta được $x=2cm$

Trạng thái ban đầu: \(\left\{{}\begin{matrix}p_0\left(atm\right)\\T_0\left(K\right)\end{matrix}\right.\)
Trạng thái sau: \(\left\{{}\begin{matrix}p_1=p_0+\dfrac{1}{360}p_0\left(atm\right)\\T_1=T_0+274\left(K\right)\end{matrix}\right.\) Do \(1^oC=273+1=274K\)
Quá trình đẳng tích:
\(\dfrac{p_0}{T_0}=\dfrac{p_1}{T_1}\Rightarrow\dfrac{p_0}{T_0}=\dfrac{p_0+\dfrac{1}{360}p_0}{T_0+274}\Rightarrow\dfrac{T_0}{T_0+274}=\dfrac{p_0}{p_0+\dfrac{1}{360}p_0}=\dfrac{360}{361}\)
\(\Rightarrow T_0=98640K=98367^oC\)

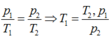
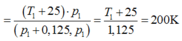
Đáp án A
- Gọi p 1 , T 1 là áp suất và nhiệt độ của khí lúc đầu
- Gọi p 2 , T 2 là áp suất và nhiệt độ khí lúc sau
Theo định luật Sác – lơ:
Với