Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) y = x3 + 3x2 + 1
Tập xác định: D = R
y’= 3x2 + 6x = 3x(x+ 2)
y’=0 ⇔ x = 0, x = -2
Bảng biến thiên:

Đồ thị hàm số:

b) Số nghiệm của phương trình \(x^3+3x^2+1=\dfrac{m}{2}\) chính là số giao điểm của (C) và đường thẳng (d): \(y=\dfrac{m}{2}\) (đường thẳng (d) vuông góc với Oy và cắt Oy tại \(\dfrac{m}{2}\) )
Từ đồ thị ta thấy:
- Với \(\dfrac{m}{2}< 1\Leftrightarrow m< 2\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với \(\dfrac{m}{2}=1\Leftrightarrow m=2\) : (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm.
- Với \(1< \dfrac{m}{2}< 5\)\(\Leftrightarrow2< m< 10\)
- Với \(\dfrac{m}{2}=5\Leftrightarrow m=10\): (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với \(\dfrac{m}{2}>5\Leftrightarrow m>10\): (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại (-2, 5), điểm cực tiểu (0, 1).
Đường thẳng đi qua hai điểm này có phương trình là: 1\(y-14=x-2\Leftrightarrow y=x+12\).
a) y = x3 + 3x2 + 1
Tập xác định: D = R
y’= 3x2 + 6x = 3x(x+ 2)
y’=0 ⇔ x = 0, x = -2
Bảng biến thiên:

Đồ thị hàm số:

b) Số nghiệm của phương trình x^3+3x^2+1=m/2chính là số giao điểm của (C) và đường thẳng (d): y=m/2 (đường thẳng (d) vuông góc với Oy và cắt Oy tại )
Từ đồ thị ta thấy:
- Với m/2<1⇔m<2: (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với m/2=1⇔ m = 2: (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm
- Với 1<m/2<5⇔ 2<m
- Với m/2=5⇔m=10: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với m/2>5⇔m>10 : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại (-2, 5), điểm cực tiểu (0, 1).
Đường thẳng đi qua hai điểm này có phương trình là: y−14=x−2⇔y=−2x+1

a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
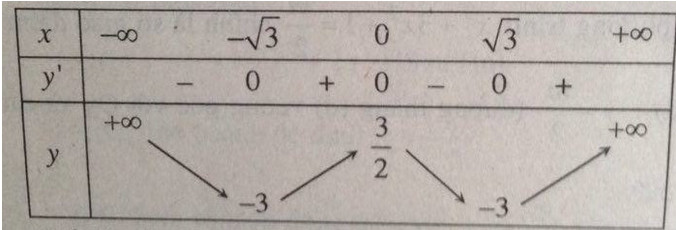
Đồ thị hàm số:
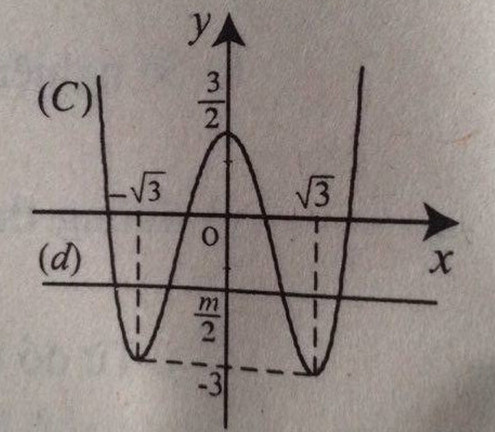
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm

a) Xét hàm số y = -x3 + 3x + 1. Tập xác định : R.
y' = -3x2 + 3 = -3(x2 - 1); y' = 0 ⇔ x = -1,x = 1.
Bảng biến thiên:
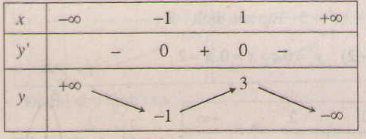
Đồ thị (C) như hình bên.

b) x3 - 3x + m = 0 ⇔ -x3 + 3x + 1 = m + 1 (1). Số nghiệm của (1) chính là số giao điểm của đồ thị (C) với đường thẳng (d) : y = m + 1.
Từ đồ thị ta thấy :
m + 1 < -1 ⇔ m < -2 : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.
m + 1 = -1 ⇔ m = -2 : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
-1 < m + 1 < 3 ⇔ -2 < m < 2 : (d) cắt (C) tại 3 điểm, (1) có 3 nghiệm.
m + 1 = 3 ⇔ m = 2 : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
m + 1 > 3 ⇔ m > 2 : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.




Số nghiệm của phương trình x 3 = b là số giao điểm của hai đồ thị hàm số y = b và y = x 3 .
Dựa vào H26 ta có đồ thị hàm số y = x 3 luôn cắt đường thẳng y = b tại một điểm duy nhất với mọi b nên phương trình x 3 = b luôn có nghiệm duy nhất với mọi b.
Số nghiệm của phương trình x 4 = b (1) là số giao điểm của hai đồ thị hàm số y = b và y = x 4 . Dựa và hình 27 ta có:
+ Với b < 0 hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.
+ Với b = 0, hai đồ thị hàm số tiếp xúc nhau tại (0,0), vậy phương trình (1) có nghiệm duy nhất x = 0.
+ Với b > 0, hai đồ thị hàm số cắt nhau tại hai điểm phân biết, vậy phương trình (1) có hai nghiệm phân biệt.