Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

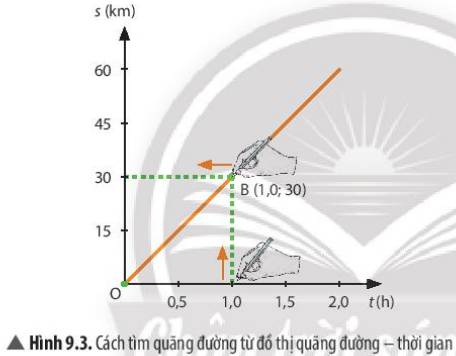
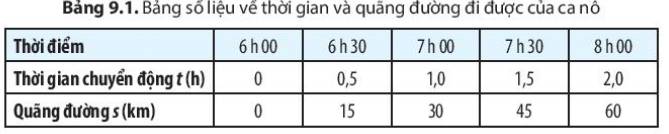
- Chọn điểm ứng với s = 60 km trên trục Os. Từ điểm này, vẽ một đường nằm ngang cắt đồ thị tại một điểm C.
- Từ C, vẽ một đường thẳng đứng cắt trục Ot, ta được t = 2,0 h.
b) Cách xác định tốc độ của ca nô:
- Từ đồ thị, xác định được ca nô đi quãng đường s = 30 km trong thời gian t = 1,0 h.
- Tính tốc độ của ca nô bằng công thức: \(v=\dfrac{s}{t}=\dfrac{30}{1,0}=\)30 km/h
a, Vận tốc : v=30(km/h) (Dựa theo đồ thị)
Thời gian đi được quãng đường 60km:
t=s/v=60/30=2(h)
b, Tốc độ của cano: v=s/t=30km/h

gọi v1 là vận tốc người đi xe đạp, v2 là vận tốc người đi xe máy
quãng đường người đi xe đạp sau 30 phút đi là:
\(s_1=v_1\cdot t_1=12\cdot\dfrac{1}{2}=6\left(km\right)\)
vị trí gặp nhau của người đi xe đạp cách A là:
\(s_g=v_1t+s_1=12\cdot t+6\left(km\right)\left(1\right)\)
vị trí gặp nhau của người đi xe máy cách A là:
\(s_g=v_2t=36\cdot t\left(km\right)\left(2\right)\)
từ (1) (2) => 12t + 6 = 36t
=> 6 = 36t - 12t => 6 = 24t => t = 0,25 (h) = 15p
thời điểm 2 xe gặp nhau là:
\(t_g=t_1+t=\dfrac{1}{2}+0,25=0,75\left(h\right)=45\left(\text{phút}\right)\)
vị trí gặp nhau cách A là:
36 x 0,25 = 9 (km)

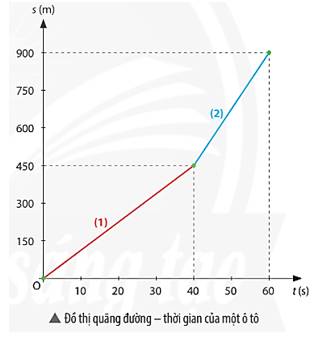
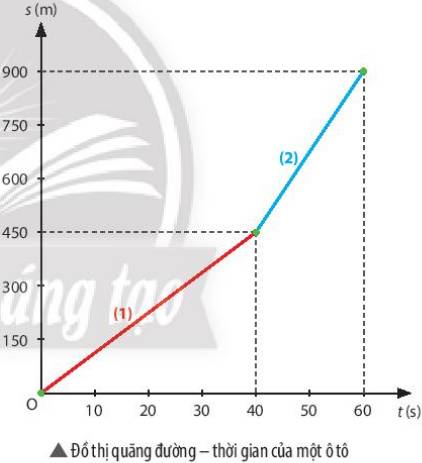
a)Từ đồ thị ta thấy t = 50 s, thì xe đi được quãng đường là s = 675 m
b) Tốc độ trung bình trên đoạn đường (1) là: \({v_{tb1}} = \frac{{\Delta {s_1}}}{{\Delta {t_1}}} = \frac{{150}}{{10}} = 15(m/s)\)
Tốc độ trung bình trên đoạn đường (2) là: \({v_{tb2}} = \frac{{\Delta {s_2}}}{{\Delta {t_2}}} = \frac{{900 - 675}}{{10}} = 22,5(m/s)\)
=> Trên đoạn đường (2), xe chuyển động nhanh hơn

Thời gian người đó đã đi đoạn đường đầu là:
6: 12 = 0,5 (giờ)
Vận tốc trung bình của người đó trên cả quãng đường là:
( 6 + 30) : ( 0,5 + 1) = 24 (km/h)
Kết luận vận tốc trung bình của người đó trên cả quãng đường là: 24km/h


tham khảo
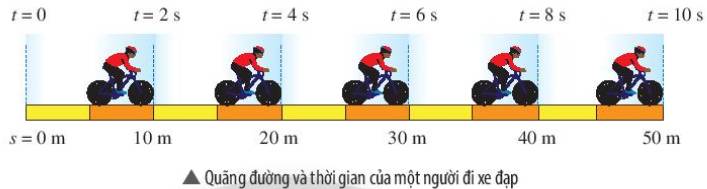
a) Bảng ghi các giá trị quãng đường s và thời gian t tương ứng của người đi xe đạp
t (s)
0
2
4
6
8
10
s (m)
0
10
20
30
40
50
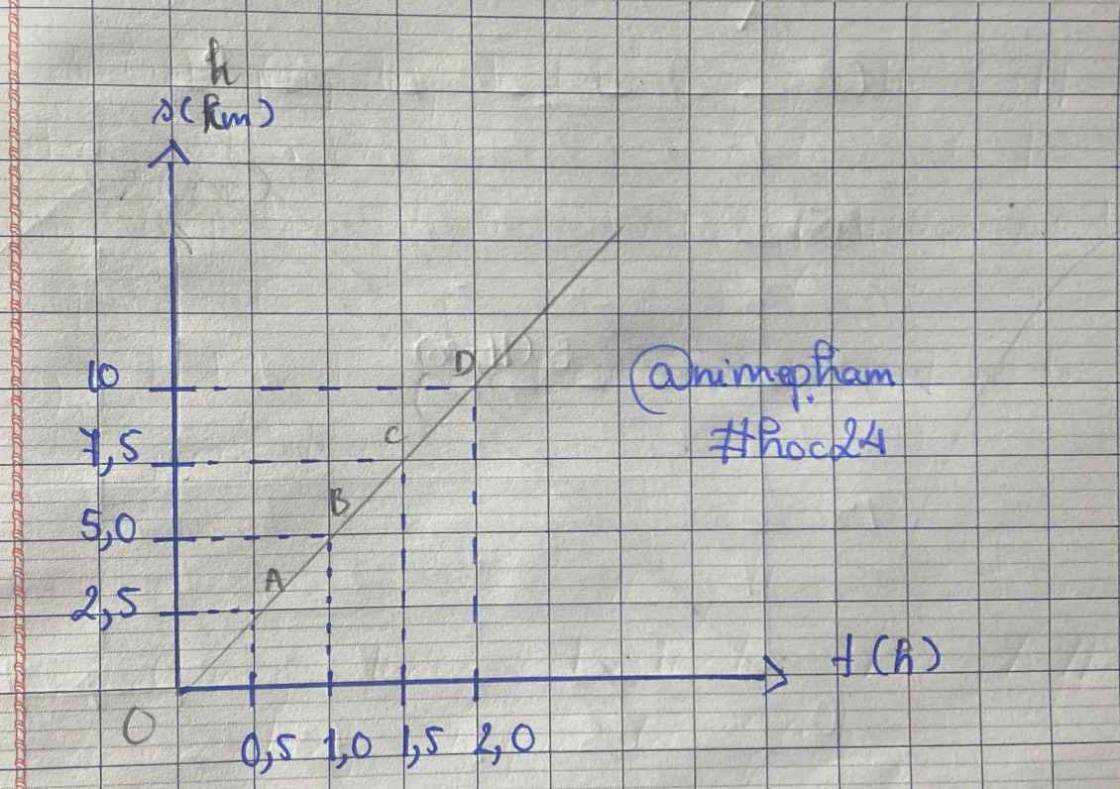
b) Vẽ đồ thị quãng đường - thời gian của người đi xe đạp