Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a.
Số tiền mua x quyển vở là: \(7000x\) (đồng)
Tổng số tiền phải trả là: \(7000x+3000\) (đồng)
Vậy công thức biểu thị tổng số tiền phải trả là:
\(y=7000x+3000\)
Do \(7000\ne0\) nên y là hàm số bậc nhất của x
b.
Số tiền phải trả khi gửi xe và mua 12 quyển vở:
\(7000.12+3000=87000\) (đồng)
c.
Nếu bạn mua 15 quyển vở thì tổng tiền phải trả là:
\(7000.12+3000=108000\) (đồng)
Số tiền này lớn hơn số tiền mang theo nên bạn Dương không thể mua 15 quyển vở
a) Biểu thức số tiền khi mua 15kg táo và 28kg nho:
\(15x+28y\)
b) Thay \(x=14000,y=17000\) vào biểu hức ta được:
- Số tiền phải trả là:
\(15\cdot14000+28\cdot17000=686000\left(đ\right)\)
a: Giá tiền cần mua là 15x+28y
b: Số tiền phải trả là:
15*14000+28*17000=686000 đồng
* Phân tích:
Vì trong 120000 Lan trả có 10000 thuế VAT nên giá gốc của hai sản phẩm không tính VAT là 110000 đồng.
| Giá gốc | Thuế VAT | |
| Hàng thứ 1 | x | 0,1.x |
| Hàng thứ 2 | 110000 – x | 0,08.(110000 – x) |
Thuế VAT của cả hai mặt hàng là 10 nghìn nên có phương trình:
0,1x + 0,08(110000 – x) = 10000.
* Giải
Gọi giá gốc của mặt hàng thứ nhất là x (0 < x < 110000 đồng).
Vì trong 120000 đồng Lan trả đã có 10000 đồng thuế VAT nên tổng giá gốc của cả hai mặt hàng chỉ bằng: 120000 – 10000 = 110000 (nghìn đồng).
⇒ Giá gốc của mặt hàng thứ hai là: 110000 – x ( đồng).
Thuế VAT của mặt hàng thứ nhất bằng: 10%.x = 0,1x (đồng).
Thuế VAT của mặt hàng thứ hai bằng: 8%.(110000 – x) = 0,08.(110000 – x) (đồng).
Thuế VAT của cả hai mặt hàng bằng: 0,1x + 0,08(110000 – x) (nghìn đồng).
Theo đề bài, tổng thuế VAT của cả hai mặt hàng là 10000 đồng nên ta có phương trình:
0,1x + 0,08(110000 – x) = 10000
⇔ 0,1x + 8800 – 0,08x = 10000
⇔ 0,02x = 1200
⇔ x = 60000 (thỏa mãn điều kiện).
Vậy không kể VAT thì giá của mặt hàng thứ nhất là 60000 đồng, giá của mặt hàng thứ hai là 110000 – 60000 = 50000 đồng.
Số tiền thật sự Lan đã trả cho hai loại hàng là:
120000 - 10% 120000 = 110000 (đồng)
Gọi x (đồng) là tiền mua loại hàng thứ nhất không kể thuế VAT (0 < x < 110000)
Tiền mua loại hàng thứ hai không kể thuế VAT: 110000 – x
Số tiền thật sự Lan đã trả cho loại hàng 1: x + 0,1x
Số tiền thật sự Lan đã trả cho loại hàng 2: 110000 – x + 0,08(110000 – x)
Ta có phương trình:
x = 60000 thỏa điều kiện.
Vậy số tiền trả cho loại hàng thứ nhất là 60000 đồng (không kể thuế VAT).
Số tiền phải trả cho loại hàng thứ hai không kể thuế VAT là:
110000 - 60000 = 50000 đồng.
Số tiền Lan đã trả cho 2 loại hàng (không gồm VAT):
120000 - 10000 = 100000 (đ)
Gọi số tiền cần trả cho loại hàng thứ nhất là a, loại hàng thứ 2 là b (đơn vị: nghìn đồng)
Ta có:
10%a + 8%b = 10 (1)
a + b = 110
\(\Rightarrow\) a = 110 - b (2)
Thế (2) vào (1), ta có:
10%(110 - b) + 8%b = 10
\(\Leftrightarrow\) 10% . 110 - 10%b + 8%b = 10
\(\Leftrightarrow\)11 - 2%b = 10
\(\Leftrightarrow\) 11 - 10 = 2%b
\(\Leftrightarrow\) 2%b = 1
\(\Leftrightarrow\) b = 50 (nghìn đồng)
\(\Rightarrow\) a = 110 - 50 = 60 (nghìn đồng)
Vậy giá tiền hai loại hàng lần lượt là 60000đ và 50000đ.
a: 8 quyển vở có giá là 8x(đồng)
7 cái bút chi có giá là 7y(đồng)
Tổng số tiền phải trả là 8x+7y(đồng)
b: 3 xấp vở có giá là: \(3\cdot10\cdot x=30x\left(đồng\right)\)
2 hộp bút có giá là \(2\cdot12\cdot y=24y\left(đồng\right)\)
Số tiền phải trả là \(30x+24y\left(đồng\right)\)
c: Hai biểu thức tìm được ở trên là đa thức
a) Để tìm đa thức biểu thị số tiền bác An phải trả cho tổng số hộp sữa đã mua, ta sẽ xác định số hộp sữa mà bác An đã mua sau khi quyết định bớt đi 2 hộp. Gọi số hộp sữa mà bác An đã mua ban đầu là x.
Sau khi bớt đi 2 hộp, số hộp sữa mà bác An đã mua là x - 2.
Giá mỗi hộp sữa đã tăng 1500 đồng, nên giá mỗi hộp sữa là y + 1500 đồng.
Vậy, số tiền bác An phải trả cho tổng số hộp sữa đã mua được biểu diễn bằng đa thức là: (x - 2)(y + 1500).
b) Nếu x = 5 (hộp) và y = 18500 (đồng), ta thay vào đa thức đã tìm được ở câu a để tính số tiền bác An phải trả.
Số tiền bác An phải trả = (5 - 2)(18500 + 1500)
= 3 * 20000
= 60000 đồng.
Vậy, nếu bác An mua 5 hộp sữa với giá 18500 đồng mỗi hộp và giá sữa tăng 1500 đồng mỗi hộp, thì bác An sẽ phải trả 60000 đồng.
a) Công thức biểu thị tổng số tiền y (đồng) bạn Dương cần phải trả cho việc gửi xe đạp và mua x quyển vở là: y = 7000.x+ 3 000 (đồng)
y là hàm số bậc nhất của x
b) Số tiền bạn Dương phải trả khi gửi xe và mua 12 quyển vở là: y = 7000. 12+ 3 000 = 87 000 (đồng)
c) Công thức biểu thị số tiền còn lại t (đồng) bạn Dương còn lại sau khi gửi xe và mua x quyển vở là:
t = 100 000 – (7000.x + 3 000) = -7000.x + 97 000 (đồng)
t là hàm số bậc nhất của x
d) Với số tiền trên, bạn Dương không thể mua được 15 quyển vở vì mua 15 quyển vở hết:
7000. 15 = 105 000 (đồng) mà bạn Dương có 100 000 nên không đủ.
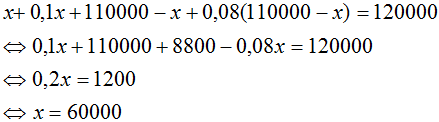
a) Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp là:
y = 200 000.x (đồng)
Nhận thấy với mỗi giá trị của x ta luôn xác định được một giá trị của y nên y là hàm số của x.
b) Số tiền mà người mua phải trả khi mua 10 quả dừa sáp là: y = 200 000 . 10 = 2000 000 (đồng)