Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sơ đồ cây:
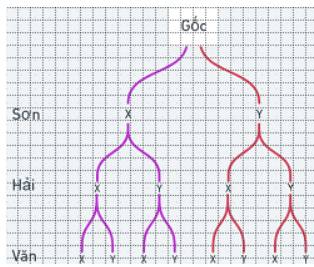
b) Dựa vào sơ đồ cây ta có \(n\left( \Omega \right) = 8\).
Gọi F là biến cố: “Hai bạn vào quán X, bạn còn lại vào quán Y”.
Ta có \(F = \left\{ {XXY;XYX;YXX} \right\}\). Suy ra \(n\left( F \right) = 3\). Vậy \(P\left( F \right) = \frac{3}{8}\).

Gọi số áo dây chuyển 1 làm được trong ngày 1 là x.
Gọi số áo dây chuyền 2 làm được trong ngày 1 là y.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}x+y=930\\118\%\cdot x+115\%\cdot y=1083\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=450\\y=480\end{matrix}\right.\)
Vậy ngày thứ nhất dây chuyền 1 may được 450 áo, dây chuyền 2 may được 480 áo.

Gọi số áo sơ mi may được trong ngày thứ nhất của dây chuyền thứ nhất và dây chuyền thứ hai lần lượt là x và y. (x > 0; y > 0)
Ngày thứ nhất cả hai dây chuyền may được 930 áo nên ta có: x + y = 930.
Ngày thứ hai:
dây chuyền thứ nhất tăng năng suất 18% nên may được x + 18%.x = 1,18.x áo
dây chuyền thứ hai tăng năng suất 15% nên may được y + 15%.y = 1,15y áo
Cả hai dây chuyền may được 1083 áo nên ta có: 1,18x + 1,15y = 1083.
Ta có hệ phương trình
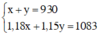
Giải hệ phương trình ta được: x = 450, y = 480
Vậy số áo sơ mi dây chuyền thứ nhất và dây chuyền thứ hai may được trong ngày thứ nhất lần lượt là 450 (áo) và 480 (áo).

a, Sơ đồ tư duy:
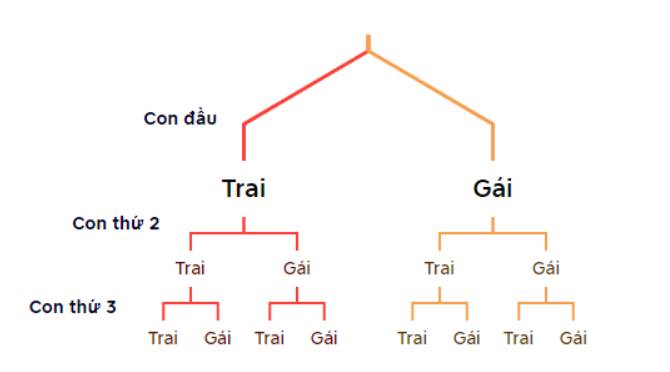
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)

Phân số chỉ số mét đường ngày thứ ba sửa được là:
\(1-\left(\frac{3}{8}+\frac{1}{3}\right)=\frac{7}{24}\)
Số mét đoạn đường dài là:
\(14\div\frac{7}{24}=48\) (m)
Đáp số: 48 mét
Chúc bạn học tốt![]()
Phân số chỉ số đoạn đường đội công dân sửa được trong hai ngày:
3/8+1/3=17/24 (mét)
Phân số chỉ số đoạn đường đội công nhân sửa trong ngày thứ 3 :
1-17/24=7/24(mét)
Số đoạn dài là:
14:7/24=48 (mét)
Đáp số:48 mét

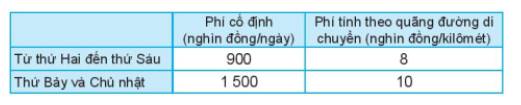
a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
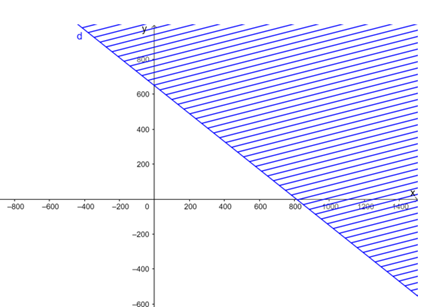
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên)
Tham khảo:
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
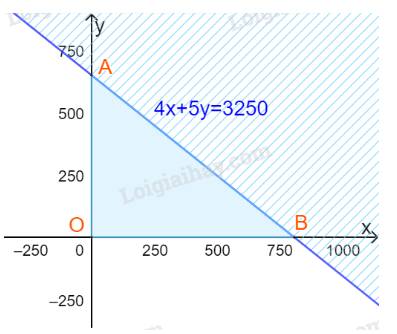
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.

Tham khảo:
a) Vẽ sơ đồ cây ba tầng.
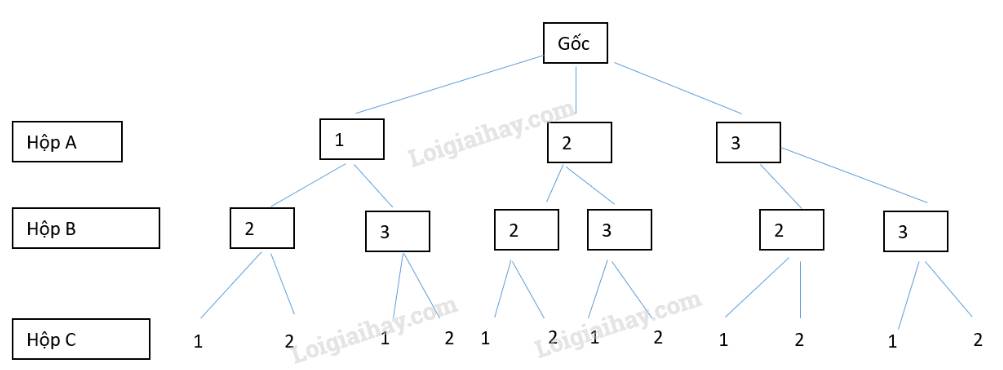
b) Chuyển qua biến cố đối: Từ sơ đồ cây xác định không gian mẫu và biến cố \(\overline M \): “Trong ba thẻ rút ra không có thẻ số 1”.
\(\begin{array}{l}\overline M = \left\{ {222;232;322;332} \right\}\\c, n(\overline M ) = 4\\P(\overline M ) = \frac{{n(\overline M )}}{{n(\Omega )}} = \frac{4}{{12}} = \frac{1}{3}\\ \Rightarrow P(M) = 1 - P(\overline M ) = 1 - \frac{1}{3} = \frac{2}{3}\end{array}\)

a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
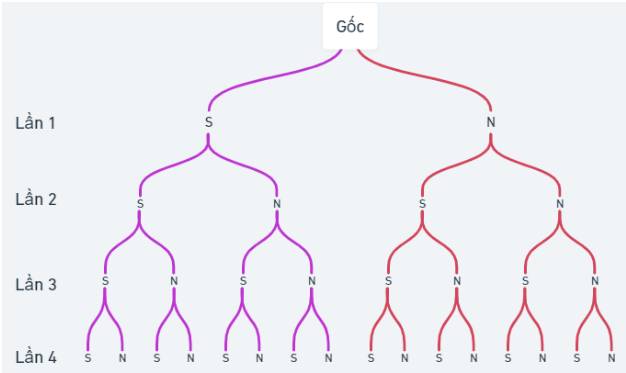
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).
a) Sơ đồ cây trong đó B là ngày có mưa và A là nhà không mưa.
Dựa vào sơ đồ cây ta thấy \(n\left( \Omega \right) = 8\).
b) Ta có \(F = \left\{ {AAB,ABA,BAA} \right\}\). Vậy \(P\left( F \right) = \frac{3}{8}\).
\(G = \left\{ {AAB,ABA,BAA,AAA} \right\}\). Vậy \(P\left( G \right) = \frac{1}{2}\).