Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\( n_{H_2O} = \dfrac{11,7}{18} = 0,65\ mol\\ n_{CO_2} = \dfrac{17,6}{44} = 0,4\ mol\\ \Rightarrow Hidrocacbon :\ C_nH_{2n+2}\\ n_{hidrocacbon} = n_{H_2O} - n_{CO_2} = 0,65 - 0,4 = 0,25(mol)\\ \Rightarrow n = \dfrac{n_{CO_2}}{n_{hidrocacbon}} = \dfrac{0,4}{0,25} = 1,6\\ 1< n=1,6<2\Rightarrow Hidrocacbon:\ CH_4,C_2H_6\\ n_{CH_4} = a\ mol ; n_{C_2H_6} = b(mol)\\ \Rightarrow a + b = 0,25 ; n_{CO_2} =a + 2b = 0,4\\ \Rightarrow a = 0,1 ; b = 0,15\\ \Rightarrow \%m_{CH_4} = \dfrac{0,1.16}{0,1.16+0,15.30}.100\% = 26,23\%\)
\(\%m_{C_2H_6} = 100\% - 26,23\% = 73,77\%\)

Đáp án B
Hidrocacbon mạch hở nên loại C. Do đó X gồm các ankadien hoặc ankin
Gọi công thức phân tử chung của 2 hidrocacbon trong Xlà CnH2n-2 (n >2)
Phản ứng:


Không biết đề có cho 2 hidrocacbon kế tiếp nhau trong dãy đồng đẳng không bạn nhỉ?
Ta có: \(n_{CO_2}=n_{CaCO_3}=\dfrac{12,5}{100}=0,125\left(mol\right)\)
m giảm = mCaCO3 - mCO2 - mH2O
⇒ mH2O = 12,5 - 0,125.44 - 3,85 = 3,15 (g)
\(\Rightarrow n_{H_2O}=\dfrac{3,15}{18}=0,175\left(mol\right)\)
Có: nH2O > nCO2 → X là ankan.
⇒ nX = 0,175 - 0,125 = 0,05 (mol)
Gọi CTPT chung của X là \(C_{\overline{n}}H_{2\overline{n}+2}\)
\(\Rightarrow\overline{n}=\dfrac{n_{CO_2}}{n_X}=2,5\)
Mà: 2 hidrocacbon kế tiếp nhau trong dãy đồng đẳng.
→ C2H6 và C3H8.

Giả sử trong 18,9 g hỗn hợp X có x mol ancol etylic và y mol hai ankan (công thức chung C n H 2 n + 2 ).
46x + (14 n + 2)y = 18,90 (1)
C 2 H 5 O H + 3 O 2 → 2 C O 2 + 3 H 2 O
x mol 2x mol 3x mol
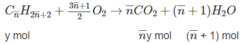
Số mol
C
O
2
= 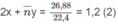
Số mol
H
2
O
= 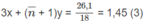
Giải hệ phương trình (1), (2), (3) tìm được x = 0,1 ; y = 0,15 ; n = 6,6
Công thức của hai ankan là C 6 H 14 và C 7 H 16 .
Đặt lượng C 6 H 14 là a mol, lượng C 7 H 16 là b mol :
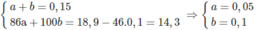
% về khối lương của
C
6
H
14
: 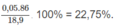
% về khối lượng của
C
7
H
16
: 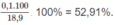

a, Gọi CTPT chung 2 ankan là \(C_{\overline{n}}H_{2\overline{n}+2}\)
\(n_{H_2O}=\dfrac{28,08}{18}=1,56\left(mol\right)\Rightarrow n_H=1,56.2=3,12\left(mol\right)\)
\(\Rightarrow n_{CO_2}=n_C=\dfrac{16,44-m_H}{12}=1,11\left(mol\right)\)
⇒ \(n_{C_{\overline{n}}H_{2\overline{n}+2}}=n_{H_2O}-n_{CO_2}=0,45\left(mol\right)\)
\(\Rightarrow\overline{n}=\dfrac{1,11}{0,45}=2,467\)
Mà: 2 ankan liên tiếp.
→ CTPT: C2H6 và C3H8.
CTCT: CH3-CH3 và CH3-CH2-CH3.
b, Có: \(30n_{C_2H_6}+44n_{C_3H_8}=16,44\left(1\right)\)
BTNT H, có: \(6n_{C_2H_6}+8n_{C_3H_8}=1,56.2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_6}=0,24\left(mol\right)\\n_{C_3H_8}=0,21\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%n_{C_2H_6}=\dfrac{0,24}{0,24+0,21}.100\%\approx53,33\%\\\%n_{C_3H_8}\approx46,67\%\end{matrix}\right.\)

nCO2 = 0,4 mol
nH2O = 0,65 mol
nH2O > nCO2 => ankan
CTB = 0,4/0,25 = 1,6 => CH4 và C2H6

Bài 1:
a, \(C_nH_{2n}+Br_2\rightarrow C_nH_{2n}Br_2\)
\(C_nH_{2n}+\dfrac{3n}{2}O_2\underrightarrow{t^o}nCO_2+nH_2O\)
\(C_3H_8+5O_2\underrightarrow{t^o}3CO_2+4H_2O\)
b, Gọi: \(\left\{{}\begin{matrix}n_{C_nH_{2n}}=x\left(mol\right)\\n_{C_3H_8}=y\left(mol\right)\end{matrix}\right.\) \(\Rightarrow x+y=\dfrac{15,68}{22,4}=0,7\left(1\right)\)
Có: \(n_{CO_2}=n.n_{C_nH_{2n}}+3n_{C_3H_8}=nx+3y=\dfrac{40,32}{22,4}=1,8\left(2\right)\)
Mà: m bình tăng = 16,8 (g) = mCnH2n = 14nx (3)
Từ (1), (2) và (3) \(\Rightarrow\left\{{}\begin{matrix}nx=1,2\\x=0,5\left(mol\right)\\y=0,2\left(mol\right)\end{matrix}\right.\)
⇒ n = 1,2:0,5 = 2,4
Mà: 2 anken đồng đẳng kế tiếp.
→ C2H4 và C3H6.
Có: \(\left\{{}\begin{matrix}28n_{C_2H_4}+42n_{C_3H_6}=16,8\\n_{C_2H_4}+n_{C_3H_6}=0,7-0,2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,3\left(mol\right)\\n_{C_3H_6}=0,2\left(mol\right)\end{matrix}\right.\)
%n cũng là %V ở cùng điều kiện nhiệt độ, áp suất.
\(\Rightarrow\left\{{}\begin{matrix}\%V_{C_2H_4}=\dfrac{0,3}{0,7}.100\%\approx42,86\%\\\%V_{C_3H_6}=\%V_{C_3H_8}=\dfrac{0,2}{0,7}.100\%\approx28,57\%\end{matrix}\right.\)
Bài 2:
a, \(n_{CO_2}=\dfrac{13,44}{22,4}=0,6\left(mol\right)\)
\(n_{H_2O}=\dfrac{6,48}{18}=0,36\left(mol\right)\)
\(\Rightarrow n_X=0,6-0,35=0,24\left(mol\right)\)
\(\Rightarrow\overline{C}=\dfrac{0,6}{0,24}=2,5\)
Mà: 2 ankin hơn kém nhau 2 C và số C nhỏ nhất có thể có là 2.
→ C2H2 và C4H6.
CTCT: C2H2: \(CH\equiv CH\)
C4H6: \(CH\equiv C-CH_2-CH_3\) hoặc \(CH_3-C\equiv C-CH_3\)
b, BTNT C, có: \(2n_{C_2H_2}+4n_{C_4H_6}=n_{CO_2}=0,6\left(1\right)\)
BTNT H, có: \(2n_{C_2H_2}+6n_{C_4H_6}=2n_{H_2O}=0,36.2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_2}=0,18\left(mol\right)\\n_{C_4H_6}=0,06\left(mol\right)\end{matrix}\right.\)
C2H2 luôn pư với AgNO3/NH3.
Ta có: \(n_{Ag_2C_2}=n_{C_2H_2}=0,18\left(mol\right)\Rightarrow m_{Ag_2C_2}=0,18.240=43,2\left(g\right)=m_{\downarrow}\)
→ C4H6 không pư.
Vậy: CTCT đúng của 2 chất là: \(CH\equiv CH\) và \(CH_3-C\equiv C-CH_3\)

\(n_{CO_2}=\dfrac{48,4}{44}=1,1\left(mol\right)\\ n_{H_2O}=\dfrac{29,7}{18}=1,65\left(mol\right)\\ Vì:n_{H_2O}>n_{CO_2}\Rightarrow hhZ:hh.ankan\\ CTTQ:C_aH_{2a+2}\\ Ta.có:1< \dfrac{n_{CO_2}}{n_{H_2O}}=\dfrac{1,65}{1,1}=1,5< 2\\ \Rightarrow hh.Z:50\%V_{CH_4},50\%V_{C_2H_6}\\ \Rightarrow\%m_{\dfrac{CH_4}{hhZ}}=\dfrac{16}{16+28}.100\approx36,364\%\\ \Rightarrow\%m_{\dfrac{C_2H_6}{hhZ}}\approx63,636\%\)