Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(\left\{{}\begin{matrix}n_{CO_2}=a\left(mol\right)\\n_{H_2O}=b\left(mol\right)\end{matrix}\right.\)
\(m_{giảm}=m_{BaCO_3}-m_{CO_2}-m_{H_2O}\)
=> 44a + 18b = 29,5 (1)
Bảo toàn C; nC = a (mol)
Bảo toàn H: nH = 2b (mol)
=> 12a + 2b = 6,3 (2)
(1)(2) => a = 0,425 (mol); b = 0,6 (mol)
Do \(n_{CO_2}< n_{H_2O}\)
=> 2 hidrocacbon là ankan
nankan = 0,6 - 0,425 = 0,175 (mol)
=> \(\overline{C}=\dfrac{0,425}{0,175}=2,43\)
Mà 2 ankan liên tiếp nhau
=> 2 ankan là C2H6 và C3H8

Đáp án B
Theo giả thiết ta có : n C O 2 = n C a C O 3 = 0 , 25 m o l
Khối lượng dung dịch giảm 7,7 gam nên suy ra :
25 - 0 , 25 . 44 - m H 2 O = 7 , 7 ⇒ m H 2 O = 6 , 3 g a m ⇒ n H 2 O = 0 , 35 m o l
Hỗn hợp X gồm hai chất đồng đẳng, đốt cháy X cho số mol nước lớn hơn số mol CO2 chứng tỏ X gồm hai ankan.
Đặt công thức phân tử trung bình của hai ankan trong X là C n ¯ H 2 n ¯ + 2
Phương trình phản ứng cháy : C n ¯ H 2 n ¯ + 2 + 3 n ¯ + 1 2 O 2 → n ¯ C O 2 + n ¯ + 1 H 2 O ( 1 )
Từ phản ứng ta suy ra : n H 2 O n C O 2 = n ¯ + 1 n ¯ = 0 , 35 0 , 25 ⇒ n ¯ = 2 , 5 h o ặ c n ¯ = n C O 2 n H 2 O - n C O 2 = 2 , 5
Với số C trung bình bằng 2,5 và căn cứ vào các phương án ta thấy hai ankan là : C2H6 và C3H8.

Đáp án A
Từ giả thiết suy ra :
n C O 2 = n C a C O 3 = 100 100 = 1 m o l ; n O 2 p ư = n O 2 b đ - n O 2 d ư = 64 32 - 11 , 2 . 0 , 4 0 , 082 . 273 = 1 , 8 m o l .
Đặt công thức phân tử trung bình của A và B là C n ¯ H 2 n ¯ + 2
Phương trình phản ứng cháy:
C n ¯ H 2 n ¯ + 2 + 3 n ¯ + 1 2 O 2 → n ¯ C O 2 + ( n ¯ + 1 ) H 2 O ( 1 ) m o l x → 3 n ¯ + 1 2 . x → n ¯ . x
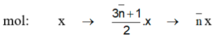


Đáp án B
Ta có nCO2 = 0,3 mol ⇒ CTrung bình = 0 , 3 0 , 2 = 1,5.
⇒ Hỗn hợp ban đầu chứa CH4 và đồng đẳng của nó.
⇒ nH2O = nCO2 + nAnkan = 0,5 mol.
Mà mBình tăng = mCO2 + mH2O = 0,3×44 + 0,5×18 = 22,2 gam.



a)
\(n_{BaCO_3}=\dfrac{78,8}{197}=0,4\left(mol\right)\)
=> \(n_{CO_2}=0,4\left(mol\right)\)
=> \(n_{H_2O}=\dfrac{22,1-0,4.44}{18}=0,25\left(mol\right)\)
Do \(n_{CO_2}>n_{H_2O}\)
=> 2 hidrocacbon thuộc dãy đồng đẳng ankin hoặc ankadien
Bảo toàn C: nC = 0,4 (mol)
Do \(\overline{C}=\dfrac{0,4}{0,15}=2,67< 3\)
=> 2 hidrocacbon thuộc dãy đồng đẳng ankin
b)
Do \(\overline{C}=2,67\)
=> Trong X có C2H2 (etin)
Giả sử A là C2H2
Gọi CTPT của B là CnH2n-2
TH1: \(\left\{{}\begin{matrix}n_A+n_B=0,15\\n_A:n_B=1:2\end{matrix}\right.\)
=> nA = 0,05 (mol); nB = 0,1 (mol)
Bảo toàn C: 2.0,05 + 0,1.n = 0,4
=> n = 3
=> B là C3H4 (propin)
TH2: \(\left\{{}\begin{matrix}n_A+n_B=0,15\\n_B:n_A=1:2\end{matrix}\right.\)
=> nA = 0,1 (mol); nB = 0,05 (mol)
Bảo toàn C: 0,1.2 + 0,05.n = 0,4
=> n = 4
=> B là C4H6
C4H6 có 2 đồng phân ankin
+ \(CH\equiv C-CH_2-CH_3\) (but-1-in)
+ \(CH_3-C\equiv C-CH_3\) (but-2-in)