Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CO2 + Ca(OH)2 → CaCO3 + H2O
0,1 0,1 0,1
2CO2 + CaCO3 + H2O → Ca(HCO3)2
0,16 – 0,1 → 0,06
=> n↓= 0,04 mol
n↓= 0,04 mol => m ↓ = 4g < 0,16 . 44 = 7,04g
=> mdd tăng = 7,04 – 4 = 3,04g
nCa(OH)2 = 2.0,05=0,1(mol)
ta có nCO2/nCa(OH)2 = 0,16/0,1 = 1,6
=> có 2 phản ứng xảy ra
CO2 + Ca(OH)2 ---> CaCO3 + H2O (1)
2CO2 +Ca(OH)2 ---> Ca(HCO3)2 (2)
bảo toàn C ta có x +2y = 0,16(3)
bảo toàn Ca ta có x +y = 0,1 (4)
từ (3) và (4) => x= 0,04(mol) y= 0,06(mol)
mCa(HCO3) = 0,06.145= 8,7(g)
m Ca(OH)2 = 0,1.57 = 5,7g
vậy khối lượng của Ca(HCO3)2 tăng 3g so với Ca(OH)2 ban đầu

Ta thấy trong X có các ancol có đặc điểm: số C = số nhóm OH
=> Khi đốt cháy X : \(n_{CO_2}=n_{C\left(X\right)}=n_{OH}=0,25mol\)
=> Khi phản ứng vớ Na => \(n_{H_2}=\frac{1}{2}n_{OH}=0,125mol\)
=> V = 2,8 lít

Phương trình ion rút gọn :
a) Ca2+ + CO32- → CaCO3 ↓
b) Fe2+ + 2OH- → Fe(OH)2↓
c) HCO3- + H+ → CO2 ↑ + H2O
d) HCO3- + OH- → H2O + CO32-
e) Không có phương trình ion rút gọn.
g) Pb(OH)2(r) + 2H+ → Pb2+ + 2H2O
h) H2PbO2(r) + 2OH- → PbO22- + 2H2O
i) Cu2+ + S2- → CuS↓.

Ta có: \(n_{COOH\left(X\right)}=n_{CO_2}=0,7mol\)
Khi đốt X có: \(n_{CO_2}=0,4mol;n_{CO_2}=0,8mol\)
Theo ĐLBT oxi có \(n_O=2n_{COOH\left(X\right)}+2n_{O_2}=2n_{CO_2}+n_{H_2O}\)
\(\Rightarrow n_{H_2O}=y=0,6mol\)

Phương trình phân tứ và ion xảy ra trong dung dịch :
a) Fe2(SO4)3 + 6NaOH → 2Fe(OH)3\(\downarrow\) + 3Na2SO4
2Fe3+ + 3SO42- + 6Na+ + 6OH- → 2Fe(OH)3\(\downarrow\)+ 6Na+ + 3SO42-
Fe3+ + 3OH- → Fe(OH)3\(\downarrow\)
b) NH4Cl + AgNO3 → NH4NO3 + AgCl↓
NH4 + Cl- + Ag+ + NO3- → NH4+ + NO3- + AgCl↓
Cl- + Ag+ → AgCl↓
c) NaF + HCl → NaCl + HF↑
Na+ + F- + H+ + Cl- → Na+ + Cl- + HF↑
F- + H+ → HF\(\uparrow\)
d) Không có phản ứng xảy ra
e) FeS(r) + 2HCl → FeCl2 + H2S ↑
FeS(r) + 2H+ + 2Cl- → Fe2+ + 2Cl- + H2S↑
FeS(r) + 2H+ \(\rightarrow\) Fe2+ + H2S↑
g) HClO + KOH \(\rightarrow\) KClO + H2O
HClO + K+ + OH- \(\rightarrow\) K+ + CIO- + H2O
HClO + OH- \(\rightarrow\) CIO- + H2O.
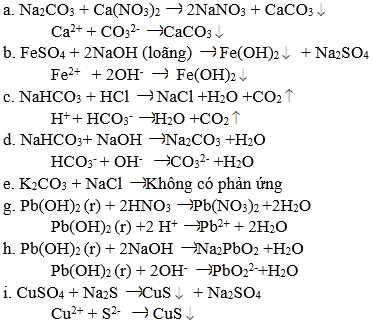
a, \(n_{CO_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
\(n_{H_2O}=\dfrac{3,6}{18}=0,2\left(mol\right)\)
Vì: nH2O > nCO2 → X là ankan.
Ta có: nX = 0,2 - 0,15 = 0,05 (mol)
Gọi CTPT của X là CnH2n+2
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_X}=3\)
→ CTPT của X là C3H8.
CTCT: CH3-CH2-CH3. Tên gọi: propan.
b, - Thu 2 sản phẩm thế monoclo.
PT: \(CH_3-CH_2-CH_3+Cl_2\underrightarrow{as}\left[{}\begin{matrix}CH_2Cl-CH_2-CH_3\\CH_3-CHCl-CH_3\end{matrix}\right.\) \(+HCl\)