Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, Gọi: CTPT chung của 2 ankin là \(C_{\overline{n}}H_{2\overline{n}-2}\)
Ta có: \(n_{CO_2}=n_{CaCO_3}=\dfrac{100}{100}=1\left(mol\right)\)
\(\Rightarrow n_{C_{\overline{n}}H_{2\overline{n}-2}}=\dfrac{1}{\overline{n}}\left(mol\right)\)
\(\Rightarrow M_{C_{\overline{n}}H_{2\overline{n}-2}}=\dfrac{13,4}{\dfrac{1}{\overline{n}}}=13,4\overline{n}\left(g/mol\right)\)
\(\Rightarrow12\overline{n}+2\overline{n}-2=13,4\overline{n}\Rightarrow\overline{n}=3,33\)
Mà: 2 ankin đồng đẳng kế tiếp.
→ C3H4 và C4H6.
\(\Rightarrow\left\{{}\begin{matrix}40n_{C_3H_4}+54n_{C_4H_6}=13,4\\3n_{C_3H_4}+4n_{C_4H_6}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n_{C_3H_4}=0,2\left(mol\right)\\n_{C_4H_6}=0,1\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{C_3H_4}=\dfrac{0,2.40}{13,4}.100\%\approx59,7\%\\\%m_{C_4H_6}\approx40,3\%\end{matrix}\right.\)
2, C3H4 có 1 CTCT: \(CH\equiv C-CH_3\), khi pư với dd AgNO3/NH3 thu kết tủa là \(AgC\equiv CCH_3\): 0,2 (mol)
\(\Rightarrow m_{C_3H_3Ag}=0,2.147=29,4\left(g\right)=m_{\downarrow}\)
→ C4H6 không pư với dd AgNO3/NH3.
→ CTCT: \(CH_3C\equiv CCH_3\)

a, Gọi CTPT chung của 2 ankin là: \(C_{\overline{n}}H_{2\overline{n}-2}\)
Ta có: \(n_{C_{\overline{n}}H_{2\overline{n}-2}}=\dfrac{46,9-14,8}{108-1}=0,3\left(mol\right)\)
\(\Rightarrow M_{C_{\overline{n}}H_{2\overline{n}-2}}=\dfrac{14,8}{0,3}=\dfrac{148}{3}\left(g/mol\right)\)
\(\Rightarrow12\overline{n}+2\overline{n}-2=\dfrac{148}{3}\Rightarrow\overline{n}=3,67\)
Mà: 2 ankin đồng đẳng kế tiếp.
→ CTPT: C3H4 và C4H6.
CTCT: C3H4: \(CH\equiv C-CH_3\)
C4H6: \(CH\equiv C-CH_2-CH_3\)
b, Ta có: \(\left\{{}\begin{matrix}40n_{C_3H_4}+54n_{C_4H_6}=14,8\\n_{C_3H_4}+n_{C_4H_6}=0,3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n_{C_3H_4}=0,1\left(mol\right)\\n_{C_4H_6}=0,2\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{C_3H_4}=\dfrac{0,1.40}{14,8}.100\%\approx27,03\%\\\%m_{C_4H_6}\approx72,97\%\end{matrix}\right.\)

a/
nX=4,48\22,4=0,2 mol
nCO2=11,2\22,4=0,5 mol
CTTQ của hh 2 anken là CnH2n
PTHH:CnH2n+3n\2O2→nCO2+nH2O
Ta có tỉ lệ: 1\0,2 =n\0,5
=>n=2,5 => công thức là C2H2, C3H6

a, Gọi: CTPT chung của 2 alcol là CnH2n+2O
\(n_{H_2}=\dfrac{0,56}{22,4}=0,025\left(mol\right)\)
\(C_nH_{2n+1}OH+Na\rightarrow C_nH_{2n+1}ONa+\dfrac{1}{2}H_2\)
Theo PT: \(n_X=2n_{H_2}=0,05\left(mol\right)\)
\(\Rightarrow M_X=\dfrac{3,35}{0,05}=67\left(g/mol\right)\)
\(\Rightarrow14n+18=67\Rightarrow n=3,5\)
Mà: 2 alcol đồng đẳng kế tiếp.
→ C3H8O và C4H10O
b, 6,7 (g) hh X có: nC3H8O + nC4H10O = 0,05.2 = 0,1 (mol) (1)
Mà: 60nC3H8O + 74nC4H10O = 6,7 (2)
Từ (1) và (2) ⇒ nC3H8O = nC4H10O = 0,05 (mol)
BTNT C, có: nCO2 = 3nC3H8O + 4nC4H10O = 0,35 (mol)
\(\Rightarrow V_{CO_2}=0,35.22,4=7,84\left(l\right)\)
BTNT H, có: nH2O = 4nC3H8O + 5nC4H10O = 0,45 (mol)
BTNT O, có: nC3H8O + nC4H10O + 2nO2 = 2nCO2 + nH2O
⇒ nO2 = 0,525 (mol)
\(\Rightarrow m_{O_2}=0,525.32=16,8\left(g\right)\)

Có ![]()
Ta có đề bài cho dữ kiện 8 gam hỗn hợp X, là số liệu dạng khối lượng không đổi thành số mol được![]() dấu hiệu của phương pháp bảo toàn khối lượng
dấu hiệu của phương pháp bảo toàn khối lượng
Bảo toàn khối lượng cho chất X ta có: mX = mC + mH
![]()
![]()
Suy ra trong X gồm C2H2 (x mol) (HC ![]() CH) và C4H6 (y mol)
CH) và C4H6 (y mol)
Ta có hệ
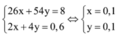
![]()
=> ankin còn lại cũng có nối ba đầu mạch.
Đáp án B.

Hỗn hơp X gồm: \(\left\{{}\begin{matrix}C_nH_{2n+2}:a\left(mol\right)\\C_mH_{2m-2}:b\left(mol\right)\end{matrix}\right.\)
Ta có: \(\dfrac{14n+2}{14m-2}=\dfrac{22}{13}\)
\(\Leftrightarrow182n+26=308m-44\)
\(\Leftrightarrow182n-308m=-70\)\(\left(I\right)\)
Khi đốt cháy hoàn toàn 0,2 mol hỗn hợp X thì:
Ta có: \(a+b=0,2\) \((II)\)
\(C_nH_{2n+2}\left(a\right)+\left(\dfrac{3n+1}{2}\right)O_2-t^o->nCO_2\left(an\right)+\left(n+1\right)H_2O\left(an+a\right)\)
\(C_mH_{2m-2}\left(b\right)+\left(\dfrac{3m-1}{2}\right)O_3-t^o->mCO_3\left(bm\right)+\left(m-1\right)H_2O\left(bm-b\right)\)
\(n_{CO_2}=0,5\left(mol\right)\)
\(\Rightarrow an+bm=0,5\)\((III)\)
\(n_{H_2O}=0,5\left(mol\right)\)
\(\Rightarrow an+bm+a-b=0,5\)\((IV)\)
Thay (III) vào (IV), ta được: \(a-b=0\) \((V)\)
Từ (II) và (V) => \(\left\{{}\begin{matrix}a+b=0,2\\a-b=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=0,1\\b=0,1\end{matrix}\right.\)
Thay vào (III), ta được: \(0,1n+0,1m=0,5\)\(\left(VI\right)\)
Từ (I) và (VI) => \(\left\{{}\begin{matrix}182n-308m=-70\\0,1n+0,1m=0,5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}n=3\\m=2\end{matrix}\right.\)
\(\Rightarrow A\left\{{}\begin{matrix}C_3H_8\\C_2H_2\end{matrix}\right.\)