Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(C+O_2\rightarrow CO_2\)(ĐK: t độ)
x x x
\(S+O_2\rightarrow SO_2\)(ĐK: t độ)
y y y
b: \(n_{O_2}=\dfrac{11.2}{22.4}=0.5\left(mol\right)\)
Theo đề, ta có hệ:
12x+32y=10 và x+y=0,5
=>x=0,3 và y=0,2
\(m_C=0.3\cdot12=3.6\left(g\right)\)
\(m_S=0.2\cdot32=6.4\left(g\right)\)
c: \(n_{CO_2}=n_C=0.3\left(mol\right)\)
\(n_{SO_2}=n_S=0.2\left(mol\right)\)
\(V_{khí}=22.4\left(0.3+0.2\right)=11.2\left(lít\right)\)
\(n_{O_2}=\dfrac{11,2}{22,4}=0,5\left(mol\right)\)
PTHH :
\(C+O_2\rightarrow\left(t^o\right)CO_2\)
x x x
\(S+O_2\rightarrow\left(t^o\right)SO_2\)
y y y
Gọi n C = x
n S = y (mol)
Ta có hệ PT :
\(\left\{{}\begin{matrix}12x+32y=10\\x+y=0,5\end{matrix}\right.\)
\(\rightarrow x=0,3;y=0,2\)
\(m_C=0,3.12=3,6\left(g\right)\)
\(m_S=0,2.32=6,4\left(g\right)\)
\(c,V_{hhk}=\left(0,3+0,2\right).22,4=11,2\left(l\right)\)

a, \(CH_4+2O_2\underrightarrow{^{t^o}}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{^{t^o}}2CO_2+2H_2O\)
b, Gọi: \(\left\{{}\begin{matrix}n_{CH_4}=x\left(mol\right)\\n_{C_2H_4}=y\left(mol\right)\end{matrix}\right.\) \(\Rightarrow x+y=\dfrac{4,48}{22,4}=0,2\left(mol\right)\left(1\right)\)
Theo PT: \(n_{O_2}=2n_{CH_4}+3n_{C_2H_4}=2x+3y=\dfrac{15,68}{22,4}=0,7\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=-0,1\\y=0,3\end{matrix}\right.\)
Đến đây thì ra số mol âm, bạn xem lại đề nhé.

a, nBr2 = 8/160 = 0,05 (mol)
PTHH: C2H4 + Br2 -> C2H4Br2
Mol: 0,05 <--- 0,05 <--- 0,05
Vhh khí = 2,8/22,4 = 0,125 (mol)
%VC2H4 = 0,05/0,125 = 40%
%CH4 = 100% - 40% = 60%
b, nCH4 = 0,125 - 0,05 = 0,075 (mol)
PTHH: C2H4 + 3O2 -> (t°) 2CO2 + 2H2O
Mol: 0,05 ---> 0,15
CH4 + 2O2 -> (t°) CO2 + 2H2O
Mol: 0,075 ---> 0,15
Vkk = (0,15 + 0,15) . 5 . 22,4 = 33,6 (l)

Gọi nCH4=a mol nH2=b mol
nhh khí=a+b=11,2/22,4=0,5
CH4 +2O2=>CO2 +2H2O
a mol =>2a mol
2H2+ O2 =>2H2O
b mol =>b mol
nH2O=2a+b=16,2/18=0,9 mol
=>a=0,4 và b=0,1 mol
%VCH4 trong hh bđ=0,4/0,5.100%=80%
%VH2=20%
a) PTHH: \(CH_4+O_2\) \(\underrightarrow{t^o}\) \(CO_2+2H_2O\)
\(2H_2+O_2\) \(\underrightarrow{t^o}\) \(2H_2O\)
b) \(n_{h_2khí}=\frac{11,2}{22,4}=0,5\left(mol\right)\)
\(n_{H_2O}=\frac{16,2}{18}=0,9\left(mol\right)\)
Gọi số mol của \(CH_4;H_2\) trong hỗn hợp đầu lần lượt là x, y (mol).
ĐK: \(0< x;y< 0,5\) \(\Rightarrow x+y=0,5\)
Theo PTHH ta có:\(n_{H_2O}=2x+y\Rightarrow\)Theo bài ra ta có hệ phương trình:
\(\begin{cases}x+y=0,5\\2x+y=0,9\end{cases}\)
\(\Rightarrow\begin{cases}2x+2y=1\\2x+y=0,9\end{cases}\)
\(\Rightarrow\begin{cases}x=0,4\\y=0,1\end{cases}\)
\(V_{CH_4}=0,4.22,4=8,96\left(lít\right)\)
\(V_{H_2}=0,1.22,4=2,24\left(lít\right)\)
\(\%CH_4=\frac{8,96}{11,2}.100\%=80\%\)
\(\%H_2=\frac{2,24}{11,2}.100\%=20\%\)

a)
\(n_{Br_2}=\dfrac{8}{160}=0,05\left(mol\right)\)
PTHH: C2H4 + Br2 --> C2H4Br2
0,05<-0,05
=> \(n_{CH_4}=\dfrac{3,36}{22,4}-0,05=0,1\left(mol\right)\)
\(\%m_{CH_4}=\dfrac{0,1.16}{0,1.16+0,05.28}.100\%=53,33\%\)
\(\%m_{C_2H_4}=\dfrac{0,05.28}{0,1.16+0,05.28}.100\%=46,67\%\)
b)
PTHH: CH4 + 2O2 --to--> CO2 + 2H2O
0,1-->0,2
C2H4 + 3O2 --to--> 2CO2 + 2H2O
0,05--->0,15
=> \(V_{O_2}=\left(0,2+0,15\right).22,4=7,84\left(l\right)\)

a, \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(2C_2H_2+5O_2\underrightarrow{t^o}4CO_2+2H_2O\)
Ta có: \(n_{CH_4}+n_{C_2H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\left(1\right)\)
\(n_{CO_2}=n_{CH_4}+2n_{C_2H_2}=\dfrac{7,84}{22,4}=0,35\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,25\left(mol\right)\\n_{C_2H_2}=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,25.22,4}{6,72}.100\%\approx83,33\%\\\%V_{C_2H_2}\approx16,67\%\end{matrix}\right.\)
Theo PT: \(n_{O_2}=2n_{CH_4}+\dfrac{5}{2}n_{C_2H_2}=0,625\left(mol\right)\Rightarrow m_{O_2}=0,625.32=20\left(g\right)\)

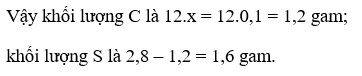
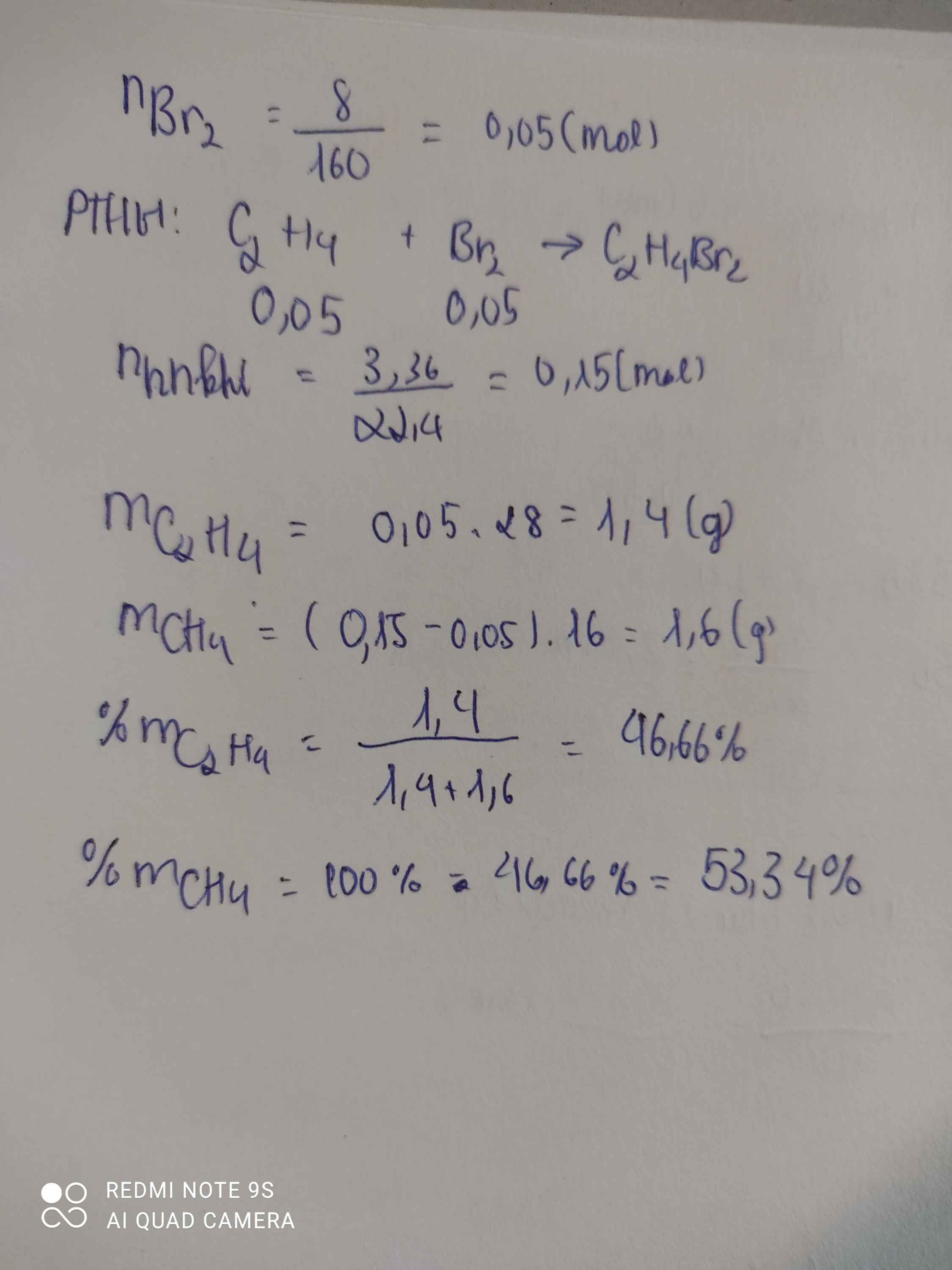
a, \(C+O_2\underrightarrow{t^o}CO_2\)
\(S+O_2\underrightarrow{t^o}SO_2\)
b, Ta có: 12nC + 32nS = 2,8 (1)
Theo PT: \(n_{O_2}=n_C+n_S=\dfrac{3,36}{22,4}=0,15\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_C=0,1\left(mol\right)\\n_S=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_C=\dfrac{0,1.12}{2,8}.100\%\approx42,86\%\\\%m_S\approx57,14\%\end{matrix}\right.\)