

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt :
nX = nY = x (mol)
CT : CnH2n+2 , CmH2m+2
nCO2 = 13.44/22.4 = 0.6 (mol)
BT C :
x(n+m) = 0.6 (1)
mhh = x(14n + 2) + x(14m + 2) = 8.8
=> 14x(n+m) + 4x = 8.8
=> 14*0.6 + 4x = 8.8
=> x = 0.1
Từ (1) => n + m = 0.6/0.1 = 6
BL : n = 2 , m = 4 => C2H6 , C4H8
n = 1 , m = 5 => CH4 , C5H12

Không biết đề có cho 2 hidrocacbon kế tiếp nhau trong dãy đồng đẳng không bạn nhỉ?
Ta có: \(n_{CO_2}=n_{CaCO_3}=\dfrac{12,5}{100}=0,125\left(mol\right)\)
m giảm = mCaCO3 - mCO2 - mH2O
⇒ mH2O = 12,5 - 0,125.44 - 3,85 = 3,15 (g)
\(\Rightarrow n_{H_2O}=\dfrac{3,15}{18}=0,175\left(mol\right)\)
Có: nH2O > nCO2 → X là ankan.
⇒ nX = 0,175 - 0,125 = 0,05 (mol)
Gọi CTPT chung của X là \(C_{\overline{n}}H_{2\overline{n}+2}\)
\(\Rightarrow\overline{n}=\dfrac{n_{CO_2}}{n_X}=2,5\)
Mà: 2 hidrocacbon kế tiếp nhau trong dãy đồng đẳng.
→ C2H6 và C3H8.

Gọi CTTQ hai ankan là $C_nH_{2n+2}$
Bảo toàn nguyên tố với C và H :
$C_nH_{2n+2} \to nCO_2 + (n + 1)H_2O$
Ta có :
$\dfrac{n}{n+1} = \dfrac{1}{1,6}$
$\Rightarrow n = 1,67$
Suy ra : 2 ankan là $CH_4$ và $C_2H_6$
Đáp án A
VCO2:VH2O=1:1,6=5:8
=>\(\dfrac{n_{CO_2}}{n_{H_2O}}=\dfrac{5}{8}\)
Giả sử \(n_{CO_2}=1\left(mol\right)\)
=>nC=1(mol); \(n_{H_2O}=1.6\left(mol\right)\)
=>nH=1,6*2=3,2(mol)
Vì nH2O>nCO2 nên tạo ra ankan
\(n_A=1.6-1=0.6\left(mol\right)\)
nO(H2O)=1,6(mol); nO(CO2)=2(mol)
\(n_{O_2\left(pư\right)}=n_{CO_2}+\dfrac{1}{2}\cdot n_{H_2O}=1+\dfrac{1}{2}\cdot1.6=1.8\left(mol\right)\)
\(C_{\overline{n}}H_{2\overline{n}+2}+O_2\rightarrow\overline{n}CO_2+\left(\overline{n}+1\right)H_2O\)
Số C trug bình là 1/0,6=5/3=1,65
=>CH4 và C2H6

Đáp án B
Định hướng tư duy giải
Để ý các chất trong X đều có 6 nguyên tử H.
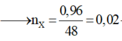
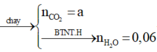
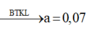
Và
![]()
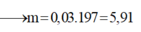

Ta có: \(\left\{{}\begin{matrix}\overline{M}_{hhkhí}=0,6\cdot29=17,4\\n_{hhkhí}=\dfrac{3,36}{22.4}=0,15\left(mol\right)\end{matrix}\right.\)
Theo phương pháp đường chéo: \(\dfrac{n_{CH_4}}{n_{C_2H_4}}=\dfrac{53}{7}\) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,1325\left(mol\right)\\n_{C_2H_4}=0,0175\left(mol\right)\end{matrix}\right.\)
Bảo toàn nguyên tố: \(\Sigma n_{CaCO_3}=n_{CH_4}+2n_{C_2H_4}=0,1675\left(mol\right)\)
\(\Rightarrow m_{CaCO_3}=0,1675\cdot100=16,75\left(g\right)\)