Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số mol CO, CxHy trong A là a, b
=> \(a+b=\dfrac{6,72}{22,4}=0,3\)
\(n_{O_2}=\dfrac{39,2}{22,4}.20\%=0,35\left(mol\right)\)
\(n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\)
\(n_{H_2O}=\dfrac{1,8}{18}=0,1\left(mol\right)\)
Bảo toàn C: a + bx = 0,4
Bảo toàn H: by = 0,2
Bảo toàn O: a + 0,7 = 0,8 + 0,1 => a = 0,2 (mol) => b = 0,1 (mol)
=> bx = 0,2 (mol)
\(\left\{{}\begin{matrix}x=\dfrac{0,2}{b}=\dfrac{0,2}{0,1}=2\\y=\dfrac{0,2}{b}=\dfrac{0,2}{0,1}=2\end{matrix}\right.\)
=> CTPT: C2H2
\(\left\{{}\begin{matrix}\%V_{CO}=\dfrac{0,2}{0,3}.100\%=66,67\%\\\%V_{C_2H_2}=\dfrac{0,1}{0,3}.100\%=33,33\%\end{matrix}\right.\)

Giả sử các khí đo ở điều kiện sao cho 1 mol khi có thể tích V lít
\(n_{CO}+n_{CO_2}=\dfrac{20}{V}\)
\(n_{O_2}=\dfrac{8}{V}\left(mol\right)\)
PTHH: 2CO + O2 --to--> 2CO2
_____\(\dfrac{16}{V}\)<---\(\dfrac{8}{V}\)
=> \(\left\{{}\begin{matrix}n_{CO}=\dfrac{16}{V}\\n_{CO_2}=\dfrac{20}{V}-\dfrac{16}{V}=\dfrac{4}{V}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\%V_{CO}=\dfrac{\dfrac{16}{V}}{\dfrac{20}{V}}.100\%=80\%\\\%V_{CO_2}=\dfrac{\dfrac{4}{V}}{\dfrac{20}{V}}.100\%=20\%\end{matrix}\right.\)

Pt:
CxHy + (x + 0,25y)O2 → xCO2 + 0,5yH2O
1 → (x + 0,25y) x 0,5y
Thể tích và số mol tỉ lệ thuận nên thể tích bằng nhau thì số mol cũng bằng nhau
Theo đề bài: n(khí trước pứ) = n(khí sau pứ)
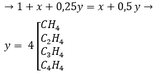

a) MX = 146g/mol
VCO2 : VH2O = 6 : 5
=> nC : nH = 3 : 5
=> CTĐGN: (C3H5Oa)n
→ (41 + 16a).n = 146 → (a; n) = (4; 2) → X: C6H10O4
b) C6H10O4 + 6,5O2 → 6CO2 + 5H2O
0,05 0,325
=> p = 7,3g
c)
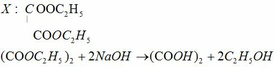

Ở cùng điều kiện nhiệt độ và áp suất, tỉ lệ số mol cũng là tỉ lệ thể tích.
BTNT O, có: \(V_{O\left(trongA\right)}+2V_{O_2}=2V_{CO_2}+V_{H_2O}\Rightarrow V_{O\left(trongA\right)}=0\)
Vậy: A chỉ gồm C và H.
Gọi CTPT của A là CxHy.
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{n_{CO_2}}{n_A}=3\\y=\dfrac{2n_{H_2O}}{n_A}=8\end{matrix}\right.\)
Vậy: CTPT cần tìm là C3H8