
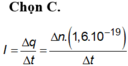
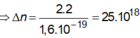
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

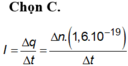
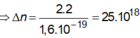
7. Hai dòng điện I1 = 3 A, I2 = 2 A chạy trong hai dây dẫn thẳng dài, song song cách nhau 50 cm theo cùng một chiều. Xác định những điểm tại đó
#Hỏi cộng đồng OLM
#Vật lý lớp 11

Điểm phải tìm nằm trong mặt phẳng chứa hai dòng điện, trong khoảng giữa hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm. Quỹ tích những điểm ấy là đường thẳng song song với hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm.
Hai dòng điện I1 = 3 A, I2 = 2 A chạy trong hai dây dẫn thẳng dài, song song cách nhau 50 cm theo cùng một chiều. Xác định những điểm tại đó
#Hỏi cộng đồng OLM
#Vật lý lớp 11

Điểm phải tìm nằm trong mặt phẳng chứa hai dòng điện, trong khoảng giữa hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm. Quỹ tích những điểm ấy là đường thẳng song song với hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm.

a) Đặt trang sách tại Cck ( điểm cực cận khi đeo kính ) thị kính có ảnh ảo tại Cc do đó :
dc = OCck = 25 cm
d'c = -OCc = - 50 cm
\(\Rightarrow f=\dfrac{d_cd'_c}{d_c+d'_c}=50cm=0,5m\Rightarrow D=\dfrac{1}{f}=2dp\)
b) Ta có :
\(d'_v=-OC_v=-500cm\Rightarrow d_v=\dfrac{d'_cf}{d'_c-f}=45,45cm\)
Vậy khi quẹo kính người đó nhìn được các vật đặt cách mắt 25 đến 45,45 cm .

bài 2
giải
đổi 20cm=0,2m
lực từ tác dụng lên một đoạn dây dẫn được xác định bằng biểu thức \(F=IB1\sin\alpha\)dòng điện vuông góc với từ trường \(\Rightarrow\sin\alpha=3\)
\(\Rightarrow B=\frac{F}{I3}=\frac{5.10^{-2}}{3.0,2}=\frac{1}{12}\left(T\right)\)
bài 3
giải
đường kính của dòng điện tròn là
\(B=2\pi.10^{-7}\frac{I}{R}\rightarrow d=2R=\frac{4.10^{-7}.I}{B}\)
\(\Rightarrow d=0,2\left(m\right)\)

Đáp án:
1154700V/m
Giải thích các bước giải:
Khi quả cầu cân bằng thì:
\(\tan a=\frac{F_d}{P}\Leftrightarrow\tan a=\frac{q^E}{mg}\\ E=\frac{\tan a.mg}{q}=1154700\left(V\text{/m}\right)\)