Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
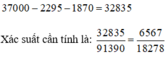
Chọn D

Đáp án B
Không gian mẫu n Ω = C 7 4
Gọi biến cố A: “Minh Anh được chọn trong 4 học sinh được chọn đi thi.”
+ Chọn Minh Anh đi thi có 1 cách.
+ Chọn 3 bạn trong 6 bạn còn lại có C 6 3 cách.
Suy ra n A = 1. C 6 3 = 20.
Vậy xác suất để Minh Anh được chọn đi thi là: P A = n A n Ω = 20 35 = 4 7 .

Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu:
n Ω = C 9 3
A: “Số học sinh nam nhiều hơn số học sinh nữ”
Ta có 2 trường hợp:
+) Chọn ra 2 nam, 1 nữ:
+) Chọn ra 3 nam, 0 nữ.
⇒ n A = C 5 2 C 4 1 + C 5 3
⇒ P A = n A n Ω = C 5 2 C 4 1 + C 5 3 C 9 3 = 25 42

Đáp án B
The đề bài ta có C n − 2 2 C n 4 = 2 C n − 2 4 C n 4 ⇔ n = 7 .

Chọn C.
Chọn ngẫu nhiên 6 học sinh trong 15 học sinh có C 15 6 cách ⇒ n Ω = C 16 5 .
Gọi X là biến cố “6 học sinh được chọn có đủ 3 khối” => biến cố đối X ¯ là “6 học sinh được chọn trong một khối hoặc hai khối”. Ta xét các trường hợp sau:
TH1. Chọn 6 học sinh từ một khối. Ta xét các trường hợp sau:
TH2. Chọn 6 học sinh từ hai khối, ta được
· 6 học sinh chọn từ khối 11 và 11 => có C 11 6 - C 6 6 cách
· 6 học sinh chọn từ khối 11 và 12 => có C 9 6 cách
· 6 học sinh chọn từ khối 12 và 10 => có C 10 6 - C 6 6 cách.
Vậy P = 1 - n X ¯ n Ω = 1 - 755 C 15 6 = 850 1001 .



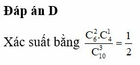
Đáp án là B