Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Áp dụng CT trả góp ta có m = 100 1 + 12 % 12 12 12 % 12 1 + 12 % 12 12 − 1 ≈ 0 , 885 triệu đồng

Đáp án A.
Gọi số tiền cô Huyền gửi ở hai ngân hàng X và Y lần lượt là x đồng và y đồng.
Theo giả thiết ta có x + y = 320 . 10 6 (1).
Tổng số tiền cả vốn lẫn lãi mà cô Huyền nhận được ở ngân hàng X sau 15 tháng (5 quý) là A = x ( 1 + 2 , 1 % ) 5 = x ( 1 , 021 ) 5 (đồng). Suy ra số tiền lãi nhận được sau 15 tháng là r A = A - x = x 1 , 021 5 - x = x 1 , 021 5 - 1 (đồng).
Tổng số tiền cả vốn lẫn lãi mà cô Huyền nhận được ở ngân hàng Y sau 9 tháng là B = y ( 1 + 0 , 37 % ) 9 = y ( 1 , 0073 ) 9 (đồng). Suy ra số tiền lãi nhận được ở ngân hàng Y sau 9 tháng là r B = B - y = y ( 1 , 0073 ) 9 - y = y 1 , 0073 9 - 1 (đồng).
Từ giả thiết, ta có:
r A + r B = 27507768 , 13 ⇔ 1 , 021 5 - 1 x + 1 . 0073 9 - 1 y = 27507768 , 13 (2)
Từ (1) và (2) có hệ:
x + y = 320 . 10 6 1 , 021 5 - 1 x + 1 , 0073 9 - 1 y = 27507768 , 13 ⇔ x = 140 . 10 6 y = 180 . 10 6 .
Vậy cô Huyền gửi ở ngân hàng X 140 triệu đồng và gửi ở ngân hàng Y 180 triệu đồng.


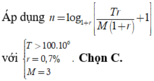
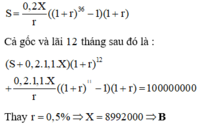

Đáp án A
Từ giả thiết ta có x + y = 10 và tổng tiền lãi nhận được là T = x 3 + 2 x + 326 y − 7 y 2
Khi đó:
T = x 3 + 2 x + 326 10 − x − 7 10 − x 2 = x 3 − 27 x 2 + 216 x + 560
Xét hàm số f x = x 3 − 27 x 2 + 216 x + 560 với x ∈ 0 ; 10 , có f ' x = 3 x 2 − 54 x + 216
Phương trình:
f ' x = 0 ⇔ 0 < x < 10 x 2 − 18 x + 72 = 0 ⇔ x = 6 ⇒ max f x = f 6