Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
Sử dụng chuẩn hóa khi tần số thay đổi.
Ta có: khi ULmax thì U L m a x = U 1 - n - 2 ⇒ U U L m a x 2 = 1 - 1 n 2 (1).
Theo đề cho: U L m a x = 4 15 U ⇒ U U L m a x 2 = 15 16 (2)
Từ (1) và (2) Suy ra: n = 4. Khi ULmax thì dùng công thức: cos φ = 2 1 + n
Hệ số công suất của đoạn mạch khi ULmax : cos φ = 2 1 + n = 2 1 + 4 = 2 5 = 10 5 .

Đáp án: C
Sử dụng chuẩn hóa khi tần số thay đổi.
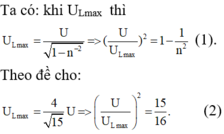
Từ (1) và (2) Suy ra: n = 4. Khi ULmax thì dùng công thức: 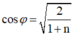
Hệ số công suất của đoạn mạch khi ULmax:
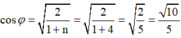

Bài 1:
Để công suát tiêu thụ trê mạch cực đại thì:
\((R+r)^2=(R_1+r)(R_1+r)\)
\(\Rightarrow (R+10)^2=(15+10)(39+10)\)
\(\Rightarrow R=25\Omega\)
Bài 2: Có hình vẽ không bạn? Vôn kế đo hiệu điện thế của gì vậy?

Công suất tiêu thụ của mạch cực đại khi xảy ra cộng hưởng P m a x = U 2 R → R = 10 Ω.
Đáp án B

Đáp án C
+ Khi L = L 0 công suất tiêu thụ của mạch là cực đại → mạch xảy ra cộng hưởng Z L = Z C
→ Khi đó
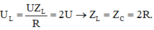
Chuẩn hóa R = 1 → Z C = 2
+ Thay đổi L để điện áp hiệu dụng trên cuộn cảm là cực đại
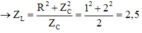
→ Công suất tiêu thụ của mạch


Chọn C.
Khi
L = L 0 ⇒ U = L 2 U ⇔ U . Z L R = 2 U ⇔ Z L = 2 R ⇔ Z C = 2 R ⇒ cos φ 0 = 1
Khi
L = L max ⇒ Z L max = R 2 + Z C 2 Z C = 2 , 5 R ⇒ cos φ 1 = 2 5 5
cos φ 1 2 cos φ 0 2 = P 1 P 0 ⇔ P 1 = 160 W .

Giả thiết ban đầu ta có cộng hưởng xảy ra --> ZL = ZC = 160
\(P_{max}=\frac{U^2}{R}\Rightarrow R=\frac{U^2}{P_{max}}=\frac{150^2}{93.75}=240\Omega\)
Giả thiết sau \(Z_{C2}=\frac{1}{100\pi\frac{10^{-3}}{\pi}}=10\Omega\)
URC vuông pha vơi Ud \(\Rightarrow\tan\varphi_{RC}\tan\varphi_d=-1\Leftrightarrow\frac{-Z_C}{R}.\frac{Z_L}{r}=-1\)
\(\Rightarrow r=\frac{10.160}{240}=\frac{20}{3}\Omega\)
Từ đó tìm Z -->I --> Các giá trị của U.

Đáp án B
Khi C=C0 , Pmax= 60W, khi đó Zc0= ZL , và Pmax= U 2 R =60
Khi C= 2C0, thì Zc= ½ ZC0 và Pmax = U 2 R 2 + 1 4 Z C 0 2 R =48
=> ZC0 = R
Khi C=1,5 C0 , ZC= 2/3 ZC0 => P= U 2 R 2 + 2 3 Z C 0 - Z L 2 R = 9U2/10R= 54(W)
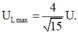 . Hệ số công suất tiêu thụ là:
. Hệ số công suất tiêu thụ là:
Bài này mình đã từng trả lời rồi, giả thiết phải là UL max= 41U/40, bạn xem lại xem chính xác không nhé.
Ta có giản đồ như sau:
AB biểu diễn điện áp trên điện trở, CD biểu diễn điện áp trên cuộn cảm, BC biểu diễn điện áp giữa 2 đầu tụ điện và AD biểu diễn điện áp trên 2 đầu đoạn mạch.
Ta có thể chọn CD=41, AD=40
Đặt BD=x;BC=41-x( Điều kiện x<41)
\(\Rightarrow AB=\sqrt{40^2-x^2}\)\(\Rightarrow\begin{cases}\tan\varphi_1=\frac{x}{\sqrt{40^2-x^2}}\\\tan\varphi_2=\frac{41-x}{\sqrt{40^2-x^2}}\end{cases}\)
Khi f biến thiên cho Uc max or UL max ta đều có tính chất:
\(\tan\varphi_1\tan\varphi_2=\frac{1}{2}\)\(\Leftrightarrow\frac{x\left(41-x\right)}{1600-x^2}=\frac{1}{2}\Leftrightarrow x=32\)
\(\Rightarrow\cos\varphi_1=\frac{AB}{AD}=0,6\)