Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
tanφAB. tanφAM = -1 ⇔ Z L - Z C R . Z L R = -1
⇔ R2=ZL(ZC – ZL) = ωL( 1 ω C - ω L )
⇔ R2= L C - ω 2 L 2 ⇔ ω = L - R 2 C L 2 C

Đáp án A
+ Cảm kháng của cuộn dây Z L = L ω = 200 Ω
Thay đổi C đến giá trị C 1 thì điện áp u vuông pha với điện áp u R L → U C m a x khi đó
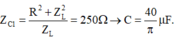

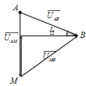
Biểu diễn vecto các điện áp. Vì U A M = U M B → AMB là tam giác cân tại M.
Từ giản đồ, ta có A ^ = B ^ = 90 0 − 15 0 = 75 0
→ φ M B = 75 0 − 15 0 = 60 0 → cos φ M B = 1 2
Đáp án C

Ta có ω 1 2 = 1 L C
Chuẩn hóa R = 1 Z L = x ⇒ Z C = x
Giả sử rằng tần số góc ω 2 = n ω 1 , khi đó ta có
U A M = U 1 2 + n x 2 1 2 + n x − x n 2 = U 1 + x 2 n 2 − 2 x 2 1 + n x 2
Để U A M không phụ thuộc vào R thì
x 2 n 2 − 2 x 2 = 0 ⇒ x = 0 n = 1 2 ⇒ f 2 = f 1 2
Đáp án D

Ta có điện áp hiệu dụng ở hai đầu đoạn mạch AM:
U A M = U R 2 + Z C 2 R 2 + Z L − Z C 2 = U 1 + Z L 2 − 2 Z L Z C R 2 + Z C 2
Để U A M không phụ thuộc vào R thì
Z L 2 − 2 Z L Z C R 2 + Z C 2 = 0 ⇒ Z L = 2 Z C
Chuẩn hóa R = 1.
→ Điện áp hiệu dụng cực đại giữa hai đầu cuộn dây
U L m a x = U R 2 + Z C 2 R = U 1 2 + 1 2 2 1 = 5 2 U
Đáp án D
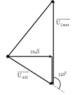
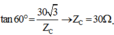
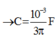

Đáp án A
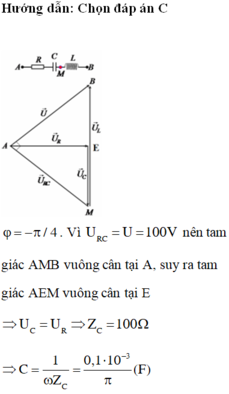
Phương pháp: Sử dụng giản đồ vecto
Cách giải:
Có:
Z C R = 1 3 ⇒ R = 3 Z C ⇒ Z L = 4 Z C
⇒ Z C = 30 Ω = 1 ω C ⇒ C = 10 - 3 3 π F