Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà \(AB=d, \hat {B} =\beta; \hat {C} =180^o-\alpha -\beta \)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

Chọn B.
Áp dụng định lí cosin trong tam giác ta có:
AB2 = AC2 + BC2 - 2BC.AC.cosC
= 2502 + 1202 - 2.250.120.cos78024’ = 64835
Suy ra AB = 255.

- Giải thích: “Đo độ cao của một ngọn núi cho kết quả là 1 235 \( \pm \)5 m” có nghĩa là
Độ cao của ngọn núi gần với 1235m và độ chính xác là 5m.
Ta có: a = 1235, d= 5.
Vì độ chính xác đến hàng đơn vị (d = 5) nên ta làm tròn a đến hàng chục.
Số quy tròn của 1235 đến hàng chục là 1240.

Sai số tương đối của kết quả các phép đo lần lượt là:

Ta có δ 3 là số nhỏ nhất trong các số trên. Vậy phép đo thứ ba có kết quả chính xác nhất.
Đáp án C

a) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right)\)
\(\cos \widehat {ABC} = \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \frac{{\left( { - 7} \right).3 + 1.3}}{{\sqrt {{{\left( { - 7} \right)}^2} + {1^2}} .\sqrt {{3^2} + {3^2}} }} = - \frac{3}{5} \Rightarrow \widehat {ABC} \approx {126^o}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right),\overrightarrow {AC} = \left( { - 10; - 2} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {104} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { - 7} \right)}^2} + {1^2}} = \sqrt {50} \end{array}\)
Vậy chu vi tam giác ABC là: \({P_{ABC}} = 2\sqrt {26} + 8\sqrt 2 \)
c) Để diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM thì M phải là trung điểm BC.
Vậy tọa độ điểm M là: \(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = \frac{{ - 9}}{2}\\\frac{{{y_B} + {y_C}}}{2} = \frac{3}{2}\end{array} \right.\). Vậy \(M\left( {\frac{{ - 9}}{2};\frac{3}{2}} \right)\)

B A C H
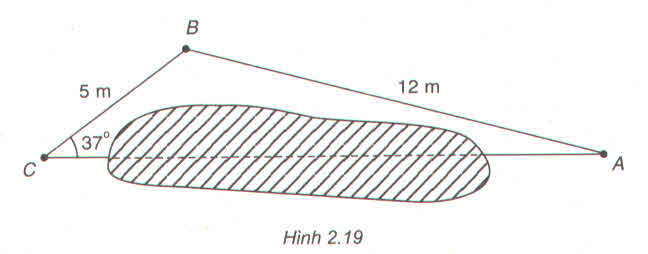
Hạ \(BH\perp AC\).
\(CH=CB.sin37^o\approx3m.\)
Áp dụng định lý Pi-ta-go trong tam giác vuông BCH:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-3^2}=4m\).
Áp dụng định lý Pi-ta-go trong tam giác vuông BHA:
\(HA=\sqrt{BC^2-BH^2}=\sqrt{12^2-4^2}=8\sqrt{2}m\).
\(AC=AH+HC=8\sqrt{2}+3m\).


Áp dụng định lý sin cho tam giác ABC, ta có:
\(2R_{giếng}=\dfrac{BC}{\sin A}=\dfrac{5}{\sin145^o}\) \(\Rightarrow R_{giếng}=\dfrac{5}{2\sin145^o}\) (m)
\(\Rightarrow S_{giếng}=\pi R_{giếng}^2=\pi\left(\dfrac{5}{2\sin145^o}\right)^2\approx59,68\left(m^2\right)\)
Khoảng cách từ M đến đường thẳng \(\Delta \) chính là độ dài đoạn MH trong đó H là hình chiếu từ M xuống \(\Delta \).
Gọi các điểm A, B, C, D như hình vẽ.
Ta có: \(OA = 3,OB = 4 \Rightarrow AB =5 \)
\(DB = 2 = \frac{1}{2}OB \Rightarrow CD = \frac{1}{2}OA = 1,5 \Rightarrow MC = 4 - 1,5 = 2,5.\)
Lại có: \(\widehat {MCH} = \widehat {BCD} = \widehat {BAO}\)
Mà: \(\sin \widehat {MCH} = \frac{{MH}}{{MC}};\sin \widehat {BAO} = \frac{{OB}}{{AB}} = \frac{4}{5}\)
\( \Rightarrow \frac{{MH}}{{2,5}} = \frac{4}{5} \Leftrightarrow MH = 2\)
Do đó kết quả đo đạc phù hợp với kết quả tính toán trong lời giải ở Ví dụ 4.