Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
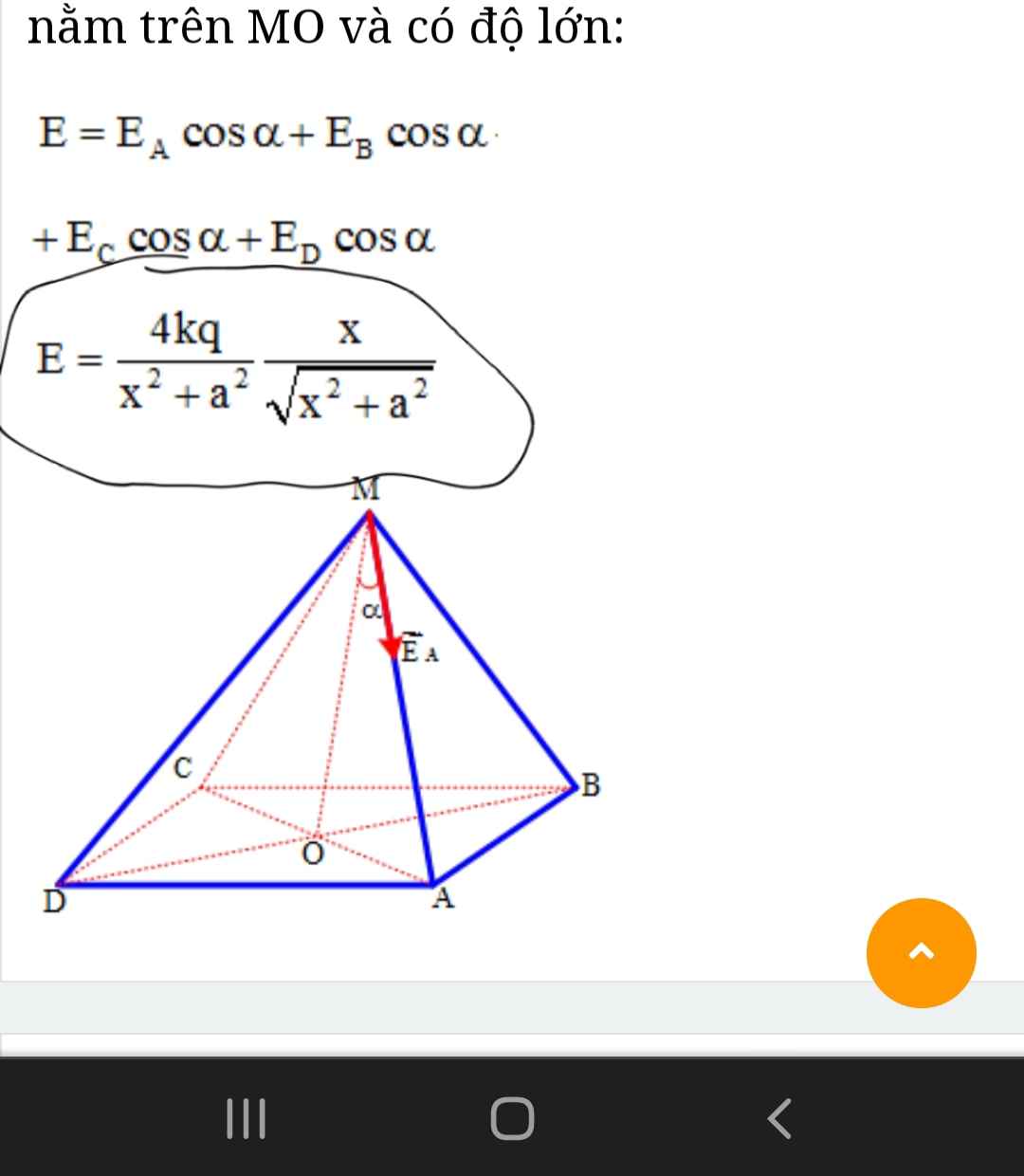
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)
+ Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈ N* là đúng với mọi n mà không thể thử trực tiếp được thì ta làm như sau:
Bước 1: Kiểm tra mệnh đề đúng với n = 1 .
Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1. Chứng minh rằng nó cũng đúng với n = k+1.
Bước 3: Kết luận mệnh đề đúng với n ∈ N*.
+ Ví dụ: Chứng minh rằng với mọi n ∈ N* ta có: n3 + 5n chia hết cho 6.
Chứng minh: Đặt P(n) = n3 + 5n.
Với n =1 ⇒ P(1) = 6 ⋮ 6
Giả sử (Pn) chia hết cho 6 đúng với n=k ≥1, nghĩa là, ta có:
P(k) = (k3 + 5k) ⋮ 6.
Ta có: P(k+1) = (k+1)3 + 5(k+1) = k3 + 3k2 + 3k + 1 + 5k + 5 = k3 + 5k + 3(k2 + k) + 6
Mặt khác, theo giả thiết quy nạp ta có: k3 + 5k ⋮6.
Hơn nữa k2 + k = k(k+1) : 2 ( hai số tự nhiên tiếp k, k +1 phải có một số chẵn do k(k+1):2).
Do vậy P(k+1)⋮6. Tức mệnh đề đúng với n = k + 1.
Theo nguyên lí quy nạp, ta có P(n) = n3 + 5n chia hết cho 6 với mọi n ∈ N*.
Ví dụ 1:
a)
Đạo hàm của biểu thức A theo x:
`A' = (√3cosx - sinx)`
Giải phương trình A' = 0:
`(√3cosx - sinx) = 0`
`⇒ √3cosx = sinx`
`⇒ 3cos^2x = sin^2x` (bình phương hai vế)
`⇒ 3(1 - sin^2x) = sin^2x` (sử dụng công thức `cos^2x = 1 - sin^2x`)
`⇒ 3 - 3sin^2x = sin^2x`
`⇒ 4sin^2x = 3`
`⇒ sin^2x = 3/4`
`⇒ sinx = ±√(3/4) = ±√3/2`
Với `sinx = √3/2`, ta có `cosx = √(1 - sin^2x) = √(1 - 3/4) = √1/4 = 1/2`
Với `sinx = -√3/2`, ta có `cosx = √(1 - sin^2x) = √(1 - 3/4) = √1/4 = 1/2`
Vậy, giá trị nhỏ nhất của biểu thức A là:
`A(min) = √3sinx + cosx = √3(√3/2) + 1/2 = 3/2 + 1/2 = 2`
Giá trị lớn nhất của biểu thức A cũng là `2`
- Quy tắc: Giả sử ta phải thực hiện hai hành động liên tiếp. Nếu hành động thứ nhất có m kết quả và ứng với mỗi kết quả đó, hành động thứ hai có n kết quả, thì có m.n kết quả của hai hành động liên tiếp ấy.
- Ví dụ:
Một lớp có 3 tổ, mỗi tổ có 6 nam và 4 nữ. Cần chọn từ mỗi tổ một người để thành lập đội thanh niên tình nguyện mùa hè xanh. Hỏi có bao nhiêu cách để lập được một đội?
Giải:
Để lập đội, từ mỗi đội ta chọn một người:
+ Có 10 cách chọn 1 người từ tổ thứ nhất
+ Có 10 cách chọn 1 người từ tổ thứ hai
+ Có 10 cách chọn 1 người từ tổ thứ ba
Từ đó, theo quy tắc nhân ta có:
10. 10. 10 = 1000 (cách chọn)
:
má m
Vô hạn nhá