Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

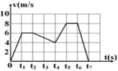
s1=v1.\(\dfrac{t}{4}\)=12,5t
s2=v2.t.0,5
s3=v3.\(\dfrac{t}{4}\)=5t
vtb=\(\dfrac{s_1+s_2+s_3}{t}\)=37,5\(\Leftrightarrow\)\(\dfrac{12,5t+v_2.t.0,5+5t}{t}\)=37,5
\(\Rightarrow\)v2=40km/h

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

a) PT x1 có dạng tổng quát là: \(x=x_0+v_0t+\dfrac{1}{2}at^2\) nên chuyển động của vật 1 là chuyển động thẳng biến đổi đều.
Căn cứ theo phương trình ta có:
+ \(x_0=0\)
+ \(v_0=-8(m/s)\)
+ \(a=2(m/s^2)\)
Do \(v_0<0\) nên t = 0 thì vật chuyển động ngược chiều dương của trục toạ độ.
Do \(v_0\) ngược dấu với \(a\) nên chuyển động đang là chuyển động chậm dần đều.
PT x2 có dạng tổng quát: \(x=x_0+v.t\) nên chuyển động của vật 1 là chuyển động thẳng đều, căn cứ theo phương trình ta suy ra được:
+ \(x_{02}=12(m)\)
+ \(v_2=5(m/s)\)
Do \(v_2>0\) nên vật 2 đang chuyển động cùng chiều dương với trục toạ độ.
b) Khoảng cách 2 vật là:
\(\Delta x = |x_1-x_2|=|t_2-13t-12|\)
\(t=2(s)\) \(\Rightarrow \Delta x = |2-13.2-12|=36(m)\)
c) Pt vận tốc của vật 2 là:
\(v=v_0+a.t=-8+2.t\) (m/s)
Vật 2 đổi chiều chuyển động khi \(v=0\Rightarrow -8+2.t=0\Rightarrow t = 4(s)\)
Ban đầu, t= 0 thì vị trí vật 2 là: \(x_2=12+5.0=12(m)\)
Khi t = 4s thì vị trí vật 2 là: \(x_2'=12+5.4=32(m)\)
Quãng đường vật 2 đi được là: \(S_2=x_2'-x_2=43-12=20(m)\)
d) Lúc t = 3s, vận tốc vật 1 là: \(v_1=-8+2.3=-2(m/s)\)
Lúc này vật 1 có vận tốc là 2m/s và đang chuyển động chậm dần đều ngược chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
e) Lúc t = 6s, vận tốc vật 1 là: \(v_1=-8+2.6=4(m/s)\)
Lúc này vật 1 có vận tốc là 4m/s và đang chuyển động nhanh dần đều cùng chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
f) Quãng đường vật 1 đi được từ 2s đến 5s là:
\(|(5^2-8.5)-(2^2-8.2)|=3(m)\)

Gia tốc do lực F1 gây ra là: \(a_1=\dfrac{\Delta v}{\Delta t} = \dfrac{5-0}{0,5} =10(m/s^2)\)
Khi tác dụng lực F2 = 2F1 thì gia tốc: \(a_2=2.a_1=2.10=20(m/s^2)\)
Vận tốc ở cuối thời điểm viên bi khi tiếp tục tác dụng lực F2 là:
\(v=v_0+a_2.t = 5 + 20.1,5 = 35(m/s)\)

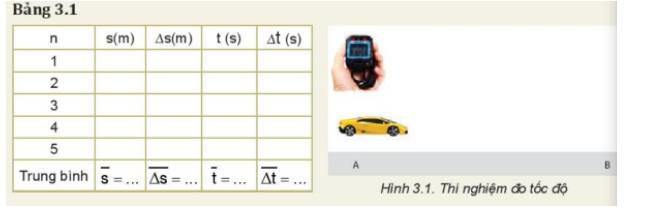
a) Nguyên nhân gây ra sự sai khác giữa các lần đo là:
- Do đặc điểm và cấu tạo của dụng cụ đo
- Do điều kiện làm thí nghiệm chưa được chuẩn
- Do thao tác khi đo
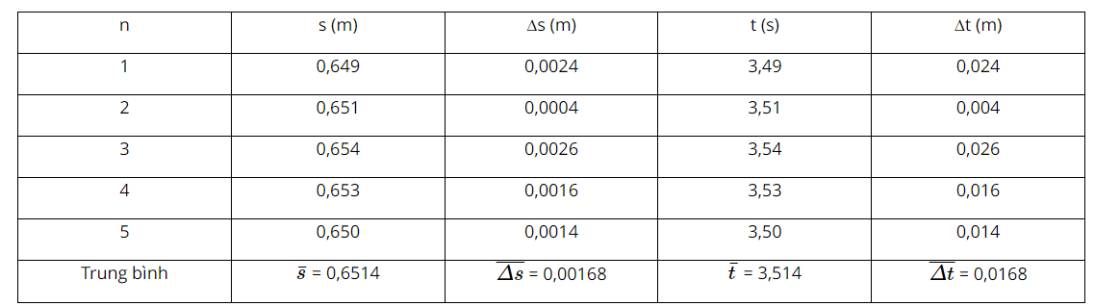
b) Ta có:
\(\overline {\Delta s} = \frac{{\left| {\overline s - {s_1}} \right| + \left| {\overline s - {s_2}} \right| + ... + \left| {\overline s - {s_5}} \right|}}{5} = 0,00168\)
\(\overline {\Delta t} = \frac{{\left| {\overline t - {t_1}} \right| + \left| {\overline t - {t_2}} \right| + ... + \left| {\overline t - {t_5}} \right|}}{5} = 0,0168\)
c) Viết kết quả đo:
Ta có:
\(\Delta s = \overline {\Delta s} + \Delta {s_{dc}} = 0,00168 + \frac{{0,001}}{2} = 0,00218\)
\(\Delta t = \overline {\Delta t} + \Delta {t_{dc}} = 0,0168 + \frac{{0,01}}{2} = 0,0218\)
Suy ra:
\(s = \overline s \pm \Delta s = 0,6514 \pm 0,00218\left( m \right)\)
\(t = \overline t \pm \Delta t = 3,514 \pm 0,0218\left( s \right)\)
d) Tính sai số tỉ đối:
\(\delta t = \frac{{\Delta t}}{{\overline t }}.100\% = \frac{{0,0218}}{{3,514}}.100\% = 0,620\)
\(\delta s = \frac{{\Delta s}}{{\overline s }}.100\% = \frac{{0,00218}}{{0,6514}}.100\% = 0,335\)
\(\delta v = \frac{{\Delta s}}{{\overline s }}.100\% + \frac{{\Delta t}}{{\overline t }}.100\% = 0,335 + 0,620 = 0,955\)
\(\Delta v = \delta v.\overline v = 0,955.\frac{{0,6514}}{{3,514}} = 0,177\left( {m/s} \right)\)
Chọn D.
Trong chuyển động thẳng nhanh dần đều, đồ thị vận tốc thời gian là đường thẳng chéo lên (v tăng đều theo t)