Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình chuyển động của xe ô tô
\(x=-5+10t\left(km,h\right)\Rightarrow x_0=-5\left(km\right)v=10\left(\dfrac{km}{h}\right)\)
vậy tọa độ ban đầu của ô tô cách gốc tọa độ O 5 km ở bên trái trục
chiều chuyển động trùng với chiều dương của trục và có tốc độ là 10 km /h
b,Đổi 30 phút =0,5 h
Tọa độ của ô tô tại thời điểm t=30 phút
\(x=-5+10\cdot0,5=0\left(km,s\right)\)
c, Quãng đường ô tô đi dc trong khoảng thời gian t1 =30 phút=0,5h đến t2=1h
\(s=10\left(1-0,5\right)=5\left(m\right)\)
bạn sửa lại nha mình đánh nhầm
dòng 3 từ dưới đếm lên :(km,h)
dòng cuối :(km)

Đường biểu diễn sự biến thiên của p theo V trong hệ toạ độ (p;V) là một đường hypebol

9. Trên một đường thẳng, tại hai điểm A và B cách nhau 10 km, có hai ô tô xuất phát cùng lúc và chuyển động cùng chiều. Ô tô xuất phát từ A có tốc độ 60 km/h và ô tô xuất phát từ B có tốc độ 40 km/h.
a) Lấy gốc tọa độ ở A, gốc thời gian là lúc xuất phát, hãy viết công thức tính quãng đường đi được và phương trình chuyển động của hai xe.
b) Vẽ đồ thị tọa độ - thời gian của hai xe trên cùng một hệ trục (x, t).
c) Dựa vào đồ thị tọa độ - thời gian để xác định vị trí và thời điểm mà xe A đuổi kịp xe B.
Trả lời:
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị
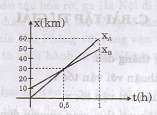
c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị

c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.

1.
Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{v_0} = 4\left( {m/s} \right);v = 16\left( {m/s} \right)\\t = 6\left( s \right)\end{array} \right.\)
Suy ra: Độ dịch chuyển là:
\(d = \frac{{\left( {4 + 16} \right).6}}{2} = 60\left( m \right)\)
2.
Ta có: Gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
Từ đồ thị ta thấy: Độ biến thiên vận tốc các khoảng thời gian bằng nhau là 2 m/s.
Xét giữa 2 thời điểm A và B:
=> \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_B} - {v_A}}}{{{t_A} - {t_B}}} = \frac{{12 - 10}}{{4 - 3}} = \frac{2}{1} = 2(m/{s^2})\)
Vậy có thể xác định được giá trị của gia tốc dựa trên đồ thị v – t.

B.cắt trục hoành tại điểm có hoành độ bằng 5