Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
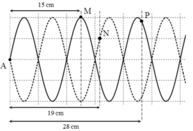
+ Sóng dừng xảy ra trên dây với 10 bụng sóng → 5λ = 0,6 m → λ = 12 cm.
+ Ta có M là bụng sóng, N và P là các điểm dao động với biên độ A N = 1 2 A A P = 3 2 A
Ta có A M – A N = 0 , 5 A M = 3 m m → A M = 6 m m .
+ Khoảng thời gian giữa hai lần liên tiếp để li độ tại M bằng biên độ tại P là Δ t = T 6 = 0 , 004 s → T = 0,024 s.
→ Tốc độ dao động cực đại của M là v M m a x = 2 π A M T = 2 π .6 0 , 024 = 500 π m m / s

chọn đáp án D
Xét khoảng cách từ một điểm tới nút gần nhất có khoảng cách là d( với
d
<
λ
4
)
ta có •
d
=
λ
12
thì biên độ dao động tại điểm đó là
A
2
•
d
=
λ
8
thì biên đọ dao động tại điểm đó là
A
2
2
d
=
λ
6
thì biên độ tại điểm đó là
A
3
2
Với A là biên độ dao động tại bụng sóng
►Đây là tb tự luận :P
Xét ba điểm M N P liên tiếp nhau trên một sợi dây mang sóng dừng
Ta có M và N dao động ngược pha nhau nên M và N đối xứng nhau qua một nút
M,N, P là ba điểm liên tiếp cùng biên độ nên ta có N và P đối xứng nhau qua một bụng
Biểu diễn trên hình ta có
M
N
2
+
N
P
2
=
λ
4
⇒
λ
=
6
c
m
GỌi M và N đối xứng nhau qua nút O
Xét Pt sóng tới O
u
1
=
A
cos
(
ω
t
)
Sóng phản xạ tại O
u
2
=
A
cos
(
ω
t
+
π
)
Xét tại điểm N
=
2
A
cos
(
π
2
+
2
π
O
N
λ
)
cos
(
ω
t
+
π
2
)
Biên độ sóng tại N
A
N
=
2
A
/
cos
(
π
2
+
2
π
O
N
λ
)
/
⇒
2
A
=
8
c
m
Như vậy biên độ tại bụng là 8 mm
Khoảng thời gian giữa hai lần sợi dây duỗi thẳng là
T
2
=
0
,
04
⇒
T
=
0
,
4
s
Vận tốc cực đại của phần tử tại bụng sóng
v
=
A
ω
=
A
2
π
T
=
628
m
m
/
s

Xem Hình II.5G.
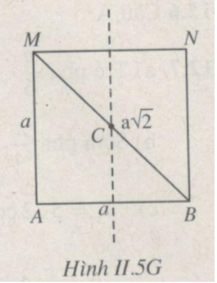
Trước hết ta tìm số vân cực đại trên toàn mặt thoáng. Đó cũng là số vân cực đại trên đoạn AB. Vì hai nguồn kết hợp dao động ngược pha nên ta có :
d 1 - d 2 = (k + 1/2) λ
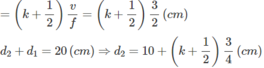
Vì 0 < d 2 < 20 (cm) ⇒ k = -13,..., -12, -1,0, 1.., 12
Bây giờ ta xét số vân cực đại trên đoạn BM.
-20 < d 2 - d 1 < 20( 2 - 1)(cm)
-20 < (k + 1/2).3/2 ≤ 2 - ( 2 - 1)
⇒ k = -13, -12 ...-1.0, 1,..., 5 ⇒ 19 điểm.

Đáp án A
HD: + Biên độ dao động của phần tử dây cách bụng sóng 1 khoảng d
A N = A M cos ( 2 πd λ = 3 m m
+ M và N thuộc hai bó sóng liên tiếp nhau nên dao động ngược pha. Gia tốc của điểm M tại thời điểm t:

Với hai đại lượng ngược pha, ta luôn có a N a M = A N A M = 1 2 ⇒ a N = 6 3 m / s 2

Đáp án A
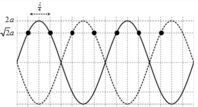
+ Các điểm cách đều nhau dao động với cùng biên độ mà không phải là bụng chỉ có thế là các vị trí cách nút gần nhất một đoạn λ 8 và dao động với biên độ bằng 2 a với 2a là biên độ của điểm bụng.
→ Khoảng cách giữa hai điểm ngoài cùng L = 7 λ 4 = 1 , 4 m → λ = 0 , 8 m → T = λ v = 0 , 8 0 , 4 = 2 s → ω = π rad/s.
→ Tốc độ cực đại của phần tử dây ứng với chuyển động của điểm bụng khi đi qua vị trí cân bằng v m a x = ω A b = π 4 2 2 = 8 π cm/s.

Đáp án A
Các điểm cách đều nhau dao động với cùng biên độ mà không phải là bụng chỉ có thế là các vị trí cách nút gần nhất một đoạn λ 8 và dao động với biên độ bằng 2 2 A b với A b là biên độ của điểm bụng
+ Khoảng cách giữa hai điểm ngoài cùng L = 7 λ 4 = 7 m → λ = 0 , 8 m; ω = π rad/s
+ Tốc độ cực đại của phần tử dây ứng với chuyển động của điểm bụng khi đi qua vị trí cân bằng v m a x = ω A b = π 4 2 2 = 8 π cm/s

Đáp án: D
HD Giải: λ = 50 2 π 50 π = 2cm
Hai nguồn ngược pha, nên điểm dao động với biên độ cực đại phải thỏa mãn: d2 – d1 = (k + 0,5)λ
Số điểm dao động với biên độ cực đại trên đoạn thẳng AB thỏa mãn điều kiện:
-AB < (k + 0,5λ) < AB
<=> -10 < 2(k + 0,5) < 10
<=> -5,5 < k < 4,5
Suy ra trên S1S2 có 10 cực đại

Đáp án C
Các điểm có cùng biên độ liên tiếp cách nhau 10 cm hoặc 20 cm thỏa mãn:
Giả sử 3 điểm có cùng biên độ là M, V, P như hình vẽ. Có 2 trường hợp có thể xảy ra như trên:
+ Trường hợp 1:
Theo lí thuyết:
Tần số góc của sóng:
Từ hình ta có:
Suy ra:
Tốc độ dao động cực đại của bụng là:
Trường hợp 2:
Theo lí thuyết:
Tần số góc của sóng:
Từ hình ta có:
Suy ra:
Tốc độ dao động cực đại của bụng là: