Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
i: Độ lớn của trận động đất là;
\(M=log\left(\dfrac{A}{A_0}\right)=log\left(\dfrac{10^{5.1}\cdot A_0}{A_0}\right)=5,1\)(richter)
ii: Độ lớn của trận động đất là:
\(M=log\left(\dfrac{A}{A_0}\right)=log\left(\dfrac{65\cdot10^3\cdot A_0}{A_0}\right)=log\left(65000\right)\simeq4,81\)(richter)
b: \(A_N=3\cdot A_P\)
\(M_N=log\left(\dfrac{A_N}{A_0}\right);M_P=log\left(\dfrac{A_P}{A_0}\right)\)
\(M_N-M_P=log\left(\dfrac{A_N}{A_0}\right)-log\left(\dfrac{A_P}{A_0}\right)\)
\(=log\left(\dfrac{A_N}{A_P}\right)=log3\simeq0,48\)
=>Trận động đất ở địa điểm N lớn hơn 0,48 độ richter

a) Tính xấp xỉ năng lượng giải toả tại tâm địa chấn ở 5 độ Richter:
Thay M = 5 vào công thức, ta có:
\(logE\approx11,4+1,5.5\approx18,9\\ \Rightarrow E\approx10^{18,9}\)
b) Tính tỷ lệ năng lượng giải toả tại tâm địa chấn ở 8 độ Richter so với tại tâm địa chấn ở 5 độ Richter:
\(logE\approx11,4+1,5.8\approx23,4\\ \Rightarrow E\approx10^{23,4}\)
`=>` Gấp khoảng 31623 lần

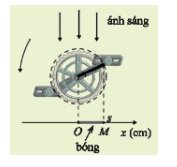
Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.

Với \({x_0}\) bất kì, ta có:
\(f'\left( {{t_0}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{19,6t - 4,9{t^2} - 19,6{t_0} + 4,9t_0^2}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \frac{{ - 4,9\left( {{t^2} - t_0^2} \right) + 19,6\left( {t - {t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \frac{{\left( {t - {t_0}} \right)\left( { - 4,9t - 4,9{t_0} + 19,6} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( { - 4,9t - 4,9{t_0} + 19,6} \right) = - 9,8{t_0} + 19,6\)
Vậy hàm số \(h = 19,6t - 4,9{t^2}\) có đạo hàm là hàm số \(h' = - 9,8{t_0} + 19,6\)
Độ cao của vật khi nó chạm đất thỏa mãn \(19,6t - 4,9{t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 4\end{array} \right.\)
Khi t = 4, vận tốc của vật khi nó chạm đất là \( - 9,8.4 + 19,6 = - 19,6\) (m/s)
Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.

a, Do \(-1\le sin\alpha\le1\Rightarrow-0,3\le v_x=0,3sin\alpha\le0,3\)
Vậy giá trị lớn nhất của \(v_x\) là 0,3m/s và giá trị nhỏ nhất là -0,3m/s
b, Ta có đồ thị hàm số:
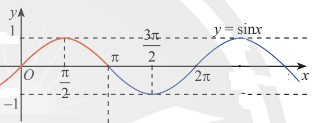
Với góc \(\alpha\in\left(0;\dfrac{\pi}{2}\right)\) hoặc \(\alpha\in\left(\dfrac{3\pi}{2};2\pi\right)\) thì \(v_x\) tăng.
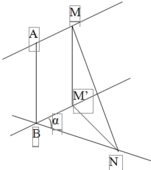
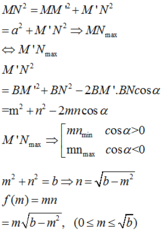
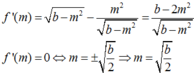
a: Khi \(A=10^{3.5}\mu m\) thì M=3,5
Khi \(A=100000\mu m\) thì M=5
Khi \(A=100\cdot10^{4.3}=10^{6.3}\mu m\) thì M=6,3
b: Nó phải thỏa mãn hệ thức \(10^M=65000\)