

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




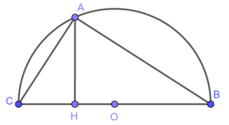
Đặt độ dài cạnh AB = x; điều kiện: x > 0
Theo bài ra theo điều (1) ta có: BC = x + 2a (3)

Bài 1
a) \(BC=125\Rightarrow BC^2=15625\)
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow\frac{AB}{3}=\frac{AC}{4}\)từ đây ta có \(\frac{AB^2}{9}=\frac{AC^2}{16}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{25}=\frac{BC^2}{25}=\frac{15625}{25}=625\)
\(\frac{AB^2}{9}=625\Rightarrow AB=75\)
\(\frac{AC^2}{16}=625\Rightarrow AC=100\)
Áp dụng hệ thức lượng trong tam giác vuông ta có
\(AB^2=BH\cdot BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{5625}{125}=45\)
\(AC^2=CH\cdot BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{10000}{125}=80\)
b.c) làm tương tự cũng áp dụng HTL trong tam giác vuông
Bài 2
Hình bạn tự vẽ
Ta có \(EH\\ AC\left(EH\perp AB;AC\perp AB\right)\Rightarrow\frac{BE}{AB}=\frac{BH}{BC}\Rightarrow BE=\frac{AB\cdot BH}{BC}\Rightarrow BE^2=\frac{AB^2\cdot BH^2}{BC^2}\)
\(\Leftrightarrow BE^2=\frac{BH\cdot BC\cdot BH^2}{BC^2}=BH^3\)
Bài 3 Đề bài này không đủ dữ kiện tính S của ABC

a.Tu gia thuyet suy ra:\(AC=20\left(cm\right)\)
Ta co:\(AH=\frac{AB.AC}{\sqrt{AB^2+AC^2}}=\frac{15.20}{\sqrt{15^2+20^2}}=20\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{225+400}=\sqrt{625}=25\left(cm\right)\)
b.Ta co:\(BH=\frac{AB^2}{BC}=\frac{225}{25}=9\left(cm\right)\)
\(CH=\frac{AC^2}{BC}=\frac{400}{25}=16\left(cm\right)\)
A B C H
a)Ta có: AB/AC=3/4 =)AC=4*AB/3=4*15/3=2
áp dụng đjnh lí Pytago tong tam giác vuông ABC, ta có:
BC^2=AB^2+AC^2
=15^2+20^2
= 225+400
=625
BC = căn 625=25
Vì ABC là tam giác vuông nên
áp dụng hệ thức lượng, ta dc
AB^2=HB*BC
hay 15^2=HB*25
HB=225/25=9
=)HC=25-9=16
và AH^2=HB*HC
=9*16=144
AH=căn 144=12
câu b là đoạn từ vì tam ABC đến HC=16 NHÉ BN
MK vẽ hình hơi xấu bn thông cảm hihi

a: xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
b: Xét ΔCAB vuông tại C có \(cosBAC=\frac{AC}{AB}=\frac12\)
nên \(\hat{BAC}=60^0\)
ΔACB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=AB^2-AC^2=\left(2R\right)^2-R^2=4R^2-R^2=3R^2\)
=>\(CB=R\sqrt3\)
c: Xét (O) có
MC,MB là các tiếp tuyến
Do đó: MC=MB
=>M nằm trên đường trung trực của CB(1)
ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1),(2) suy ra MO là đường trung trực của CB
=>MO⊥CB
mà CA⊥CB
nên CA//OM
d: Gọi I là giao điểm của MA và CH, K là giao điểm của AC và MB
ΔACB vuông tại C
=>CA⊥CB tại C
=>CB⊥AK tại C
=>ΔKCB vuông tại C
Ta có: \(\hat{MCB}+\hat{MCK}=\hat{KCB}=90^0\)
\(\hat{MBC}+\hat{MKC}=90^0\) (ΔKCB vuông tại C)
mà \(\hat{MBC}=\hat{MCB}\) (ΔMBC cân tại M)
nên \(\hat{MCK}=\hat{MKC}\)
=>MC=MK
mà MC=MB
nên MB=MK(3)
ta có: KB⊥BA
CH⊥BA
DO đó: KB//CH
Xét ΔAMK có CI//MK
nên \(\frac{CI}{MK}=\frac{AI}{AM}\left(4\right)\)
Xét ΔAMB có IH//MB
nên \(\frac{IH}{MB}=\frac{AI}{AM}\) (5)
từ (3),(4),(5) suy ra CI=IH
=>I là trung điểm của CH
=>MA đi qua trung điểm I của CH