H
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
0
TT
21 tháng 1 2022
a) \(\dfrac{x+1}{4}-\dfrac{5+2x}{8}=\dfrac{3-4x}{2}\)
⇔\(\dfrac{2\left(x+1\right)}{8}-\dfrac{5+2x}{8}=\dfrac{4\left(3-4x\right)}{8}\)
⇔ 2x + 2 - 5 - 2x = 12 -16x
⇔ 16x = 15
⇔ x = 15/16
b) \(\dfrac{4-3x}{5}-\dfrac{4-x}{10}=\dfrac{x+2}{2}\)
⇔\(\dfrac{2\left(4-3x\right)}{10}-\dfrac{4-x}{10}=\dfrac{5\left(x+2\right)}{10}\)
⇔ 8 - 6x - 4 + x = 5x + 10
⇔ 10x = -6
⇔ x = -6/10
21 tháng 1 2022
Câu 1:
x + 1/4 - 5 + 2x/8 = 3 - 4x/2
<=> 2x + 2/8 - 5 + 2x/8 = 12 - 16x/8
<=> 2x + 2 - 5 - 2x = 12 - 16x
<=> -3 = 12 - 16x <=> 15 = 16x <=> x = 15/16
Câu 2:
4 - 3x/5 - 4 - x/10 = x + 2/2
<=> 8 - 6x/10 - 4 - x/10 = 5x + 10/10
<=> 8 - 6x - 4 + x = 5x + 10
<=> 4 - 5x = 5x + 10
<=> 4 = 10x + 10 <=> 10x = -6 <=> x = -3/5
XL
2
MA
25 tháng 2 2022
ĐKXĐ: ` x ne 1 ; x ne 4`
`(2x+1)/(x^2-5x+4) + 5/(x-1) = 2/(x-4)`
`<=> (2x+1)/[(x-1)(x-4)] + [5(x-4)]/[(x-1)(x-4)] = [2(x-1)]/[(x-1)(x-4)]`
`=> 2x+1 + 5x -20 = 2x-2`
`<=> 5x = 17`
`<=> x= 17/5`(thỏa mãn ĐKXĐ)
Vậy tập nghiệm của phương trình là `S={ 17/5}`
S
18 tháng 3 2021
1,\(3x-1=0\Leftrightarrow3x=-1\Leftrightarrow x=-\dfrac{1}{3}\)
2,\(2-x=3x+1\Leftrightarrow2-1=3x+x\rightarrow1=4x\Rightarrow x=-\dfrac{1}{4}\)
S
18 tháng 3 2021
3,\(2\left(x-2\right)-1=5x\Leftrightarrow2x-4-1=5x\Leftrightarrow2x-5x=4+1\Rightarrow3x=5\Rightarrow x=\dfrac{5}{3}\)
4,\(\dfrac{x}{3}-\dfrac{x}{5}=4\Leftrightarrow\dfrac{5x}{15}-\dfrac{3x}{15}=\dfrac{60}{15}\Rightarrow5x-3x=60\Rightarrow2x=60\Rightarrow x=\dfrac{60}{2}=30\)
Y
17 tháng 1 2023
\(1,\left(dk:x\ne0,-1,4\right)\)
\(\Leftrightarrow\dfrac{9}{x+1}+\dfrac{2}{x-4}-\dfrac{11}{x}=0\)
\(\Leftrightarrow\dfrac{9x\left(x-4\right)+2x\left(x+1\right)-11\left(x+1\right)\left(x-4\right)}{x\left(x+1\right)\left(x-4\right)}=0\)
\(\Leftrightarrow9x^2-36x+2x^2+2x-11x^2+44x-11x+44=0\)
\(\Leftrightarrow-x=-44\)
\(\Leftrightarrow x=44\left(tm\right)\)
\(2,\left(đk:x\ne4\right)\)
\(\Leftrightarrow\dfrac{14}{3\left(x-4\right)}-\dfrac{2+x}{x-4}-\dfrac{3}{2\left(x-4\right)}+\dfrac{5}{6}=0\)
\(\Leftrightarrow\dfrac{14.2-6\left(2+x\right)-3.3+5\left(x-4\right)}{6\left(x-4\right)}=0\)
\(\Leftrightarrow28-12-6x-9+5x-20=0\)
\(\Leftrightarrow-x=13\)
\(\Leftrightarrow x=-13\left(tm\right)\)
24 tháng 2 2021
a) Ta có: \(2\left(3x+1\right)-4\left(5-2x\right)>2\left(4x-3\right)-6\)
\(\Leftrightarrow6x+2-20+8x>8x-6-6\)
\(\Leftrightarrow14x-18-8x+12>0\)
\(\Leftrightarrow6x-6>0\)
\(\Leftrightarrow6x>6\)
hay x>1
Vậy: S={x|x>1}
b) Ta có: \(9x^2-3\left(10x-1\right)< \left(3x-5\right)^2-21\)
\(\Leftrightarrow9x^2-30x+3< 9x^2-30x+25-21\)
\(\Leftrightarrow9x^2-30x+3-9x^2+30x-4< 0\)
\(\Leftrightarrow-1< 0\)(luôn đúng)
Vậy: S={x|\(x\in R\)}
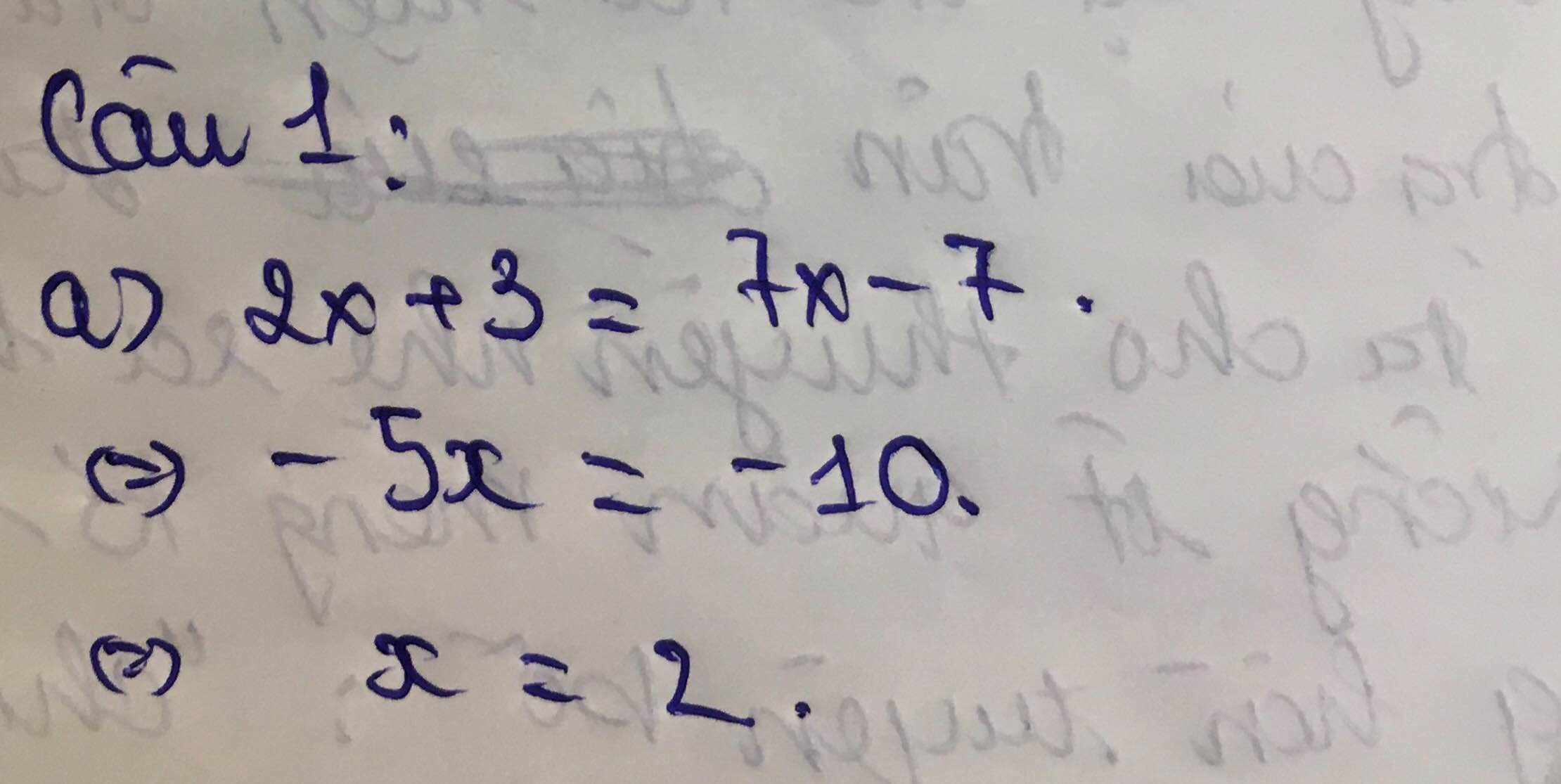
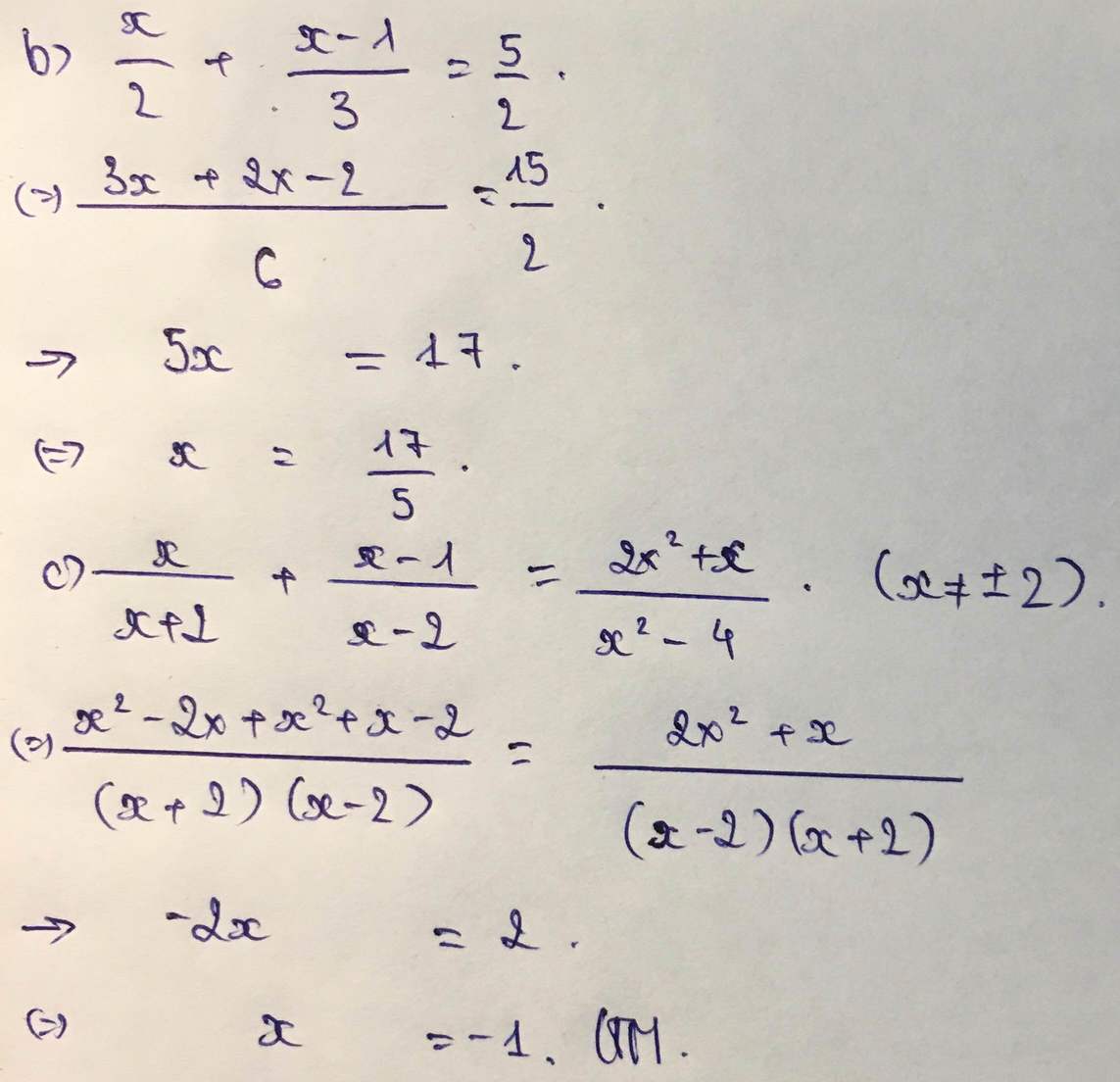
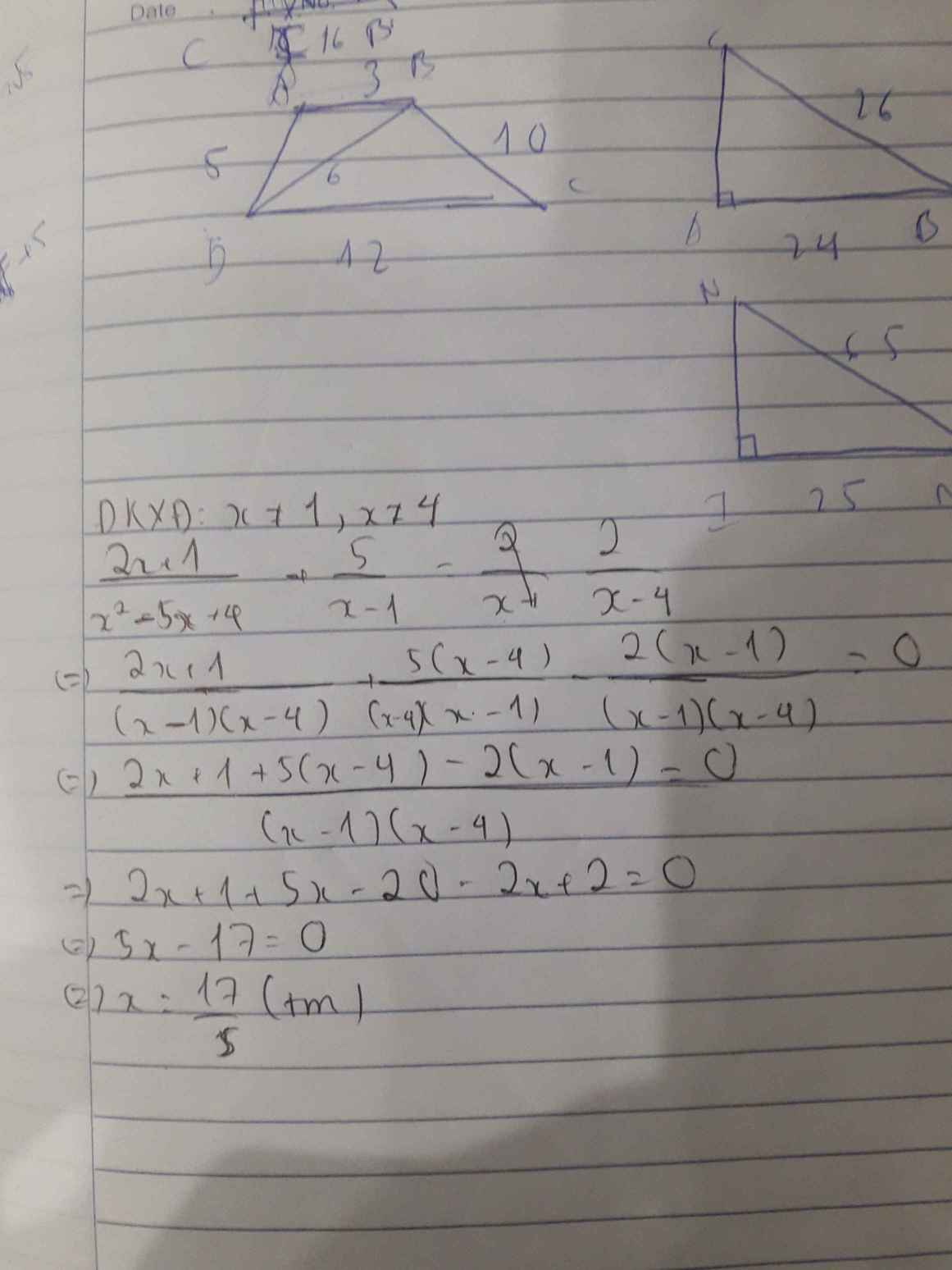
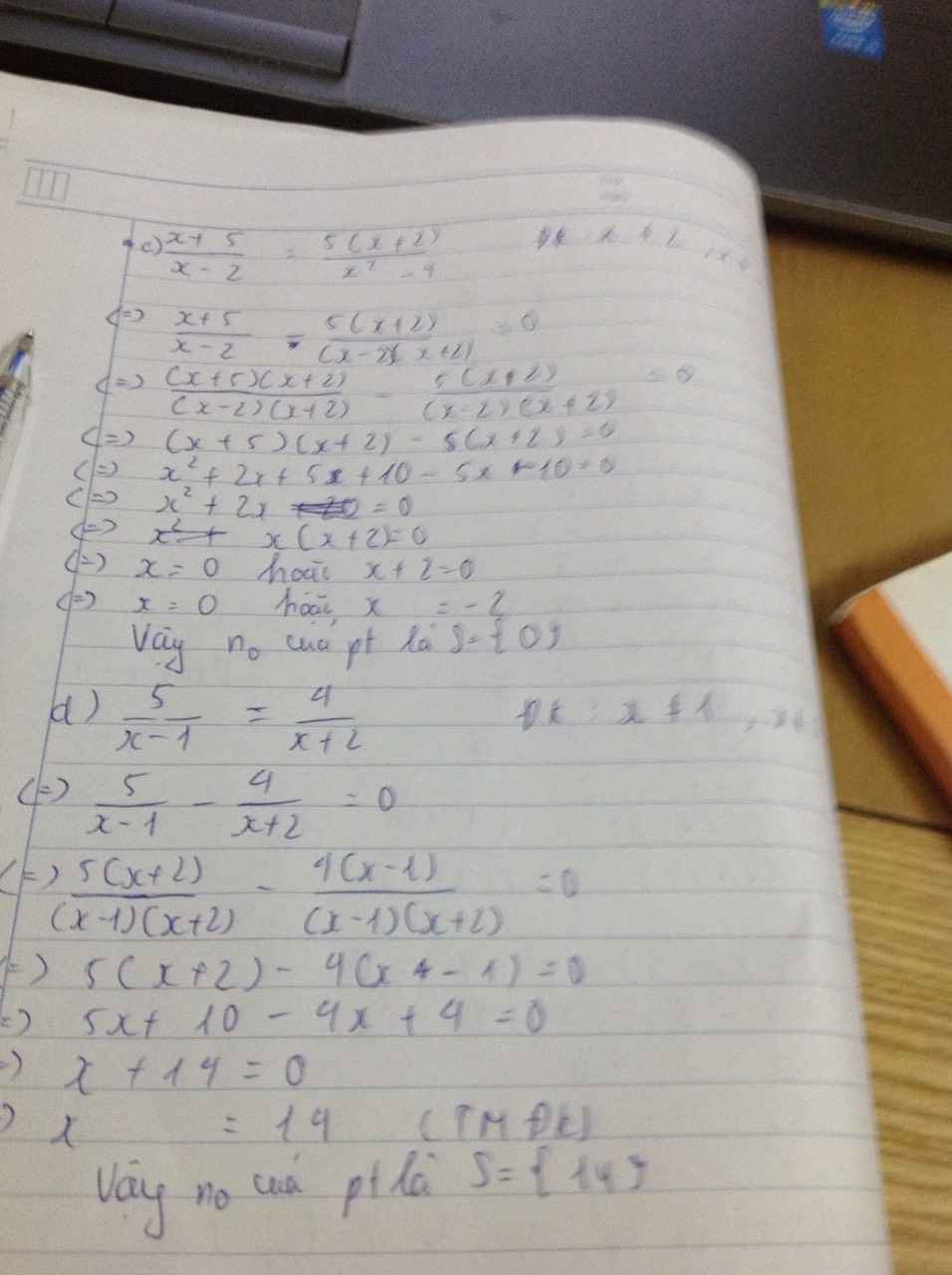
ĐKXĐ : \(x\ne4;x\ne-4\)
\(Đkxđ:\\ \Leftrightarrow\left\{{}\begin{matrix}x-4=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\\ \Rightarrow x\ne\pm4\)