
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



*1. Các trường hợp bằng nhau đã biết của hai tam giác vuông.
- Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau(theo trường hợp c.g.c)
- Nếu một cạnh của tam giác vuông này và một góc nhọn kề cạnh ấy bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( theo trường hợp g.c.g )
2. Trường hợp bằng nhau về cạnh huyền mà một cạnh góc vuông
Nếu cạnh huyền và môt cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
*1. Định lí Pytago
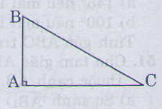
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
2. Định lí Pytago đảo.
Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.

https://123doc.org/document/1085873-20-cach-chung-minh-dinh-ly-py-ta-go.htm

Xếp các tam giác vuông = nhau như hình vẽ:
Ta có: \(S_{BCDE}=S_{AMPN}+4.S_{ABC}\)
\(\Rightarrow a^2=\left(c-d\right)^2+4.\frac{bc}{2}\)
\(\Leftrightarrow a^2=c^2-2.bc+b^2+2.bc\)
\(\Leftrightarrow a^2=c^2+b^2\)
P/s: Còn nhiều cách.
Đây cũng là một cách chứng minh được giới thiệu trong cuốn sách của Elisha Scott Loomis. Ann Condit nghĩ ra cách chứng minh này vào năm 1938 khi cô mới 16 tuổi và là sinh viên của trường trung học ở miền nam Ấn Độ.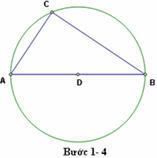
Dựng hình và kiểm tra
1. Dựng đoạn thẳng AB.
2. Vẽ trung điểm D của đoạn thẳng này
3. Vẽ đường tròn bán kính DA.
4. Vẽ đoạn BC và AC , với C là một điểm nằm trên đường tròn. Như vvậy ta đã dựng được tam giác vuông ABC vuông tại C.
5. Vẽ các hình vuông trên các cạnh của tam giác vuông ABC.
6. Vẽ các trung điểm L, M, N của các cạnh phía ngoài của các hình vuông.
7. Vẽ các đoạn DL, DM, DL.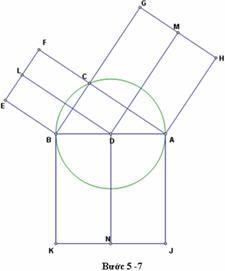
8. Vẽ đoạn FG, Vẽ tia DC, và điểm P là giao điểm cuat tia DC và đoạn FG, sau đó làm ẩn đi tia DC và hiện đoạn DP.
9. Tô màu khác nhau cho diện tích các tam giác DCF, DCG, và DBK.
Cách chứng minh này đưa ra mối liên quan giữa diện tích của các hình tam giác được tô màu với diện tích của các hình vuông trên các cạnh tam giác vuông.
Chọn menu Measure --> calculate để tính được tỉ lệ diện tích của các tam giác với các hình vuông tương ứng.
10. Đo diện tích các tam giác, và di chuyển điểm C quanh một nửa đường tròn trên đường kính AB.
Ta nhận thấy: tổng diện tích của 2 tam giác nhỏ luôn bằng diện tích của tam giác lớn hơn. Và tổng diện tích này không đổi khi điểm C chuyển động trên đường tròn. (xem hình bên dưới).
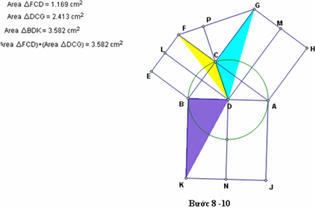
♥Trên mạng nha..Bn tham khảo nhé♥

á đù biết làm rồi cho người ta làm chi tự làm giỏi chửi tui ông cũng vậy

TK
Định lý Pytago chỉ áp dụng cho các tam giác vuông. Vì vậy, trước khi tiến hành, cần chắc chắn rằng tam giác của bạn đáp ứng đủ tiêu chí của một tam giác vuông. May mắn thay, chỉ có một tiêu chí duy nhất - để là một tam giác vuông, tam giác đó phải có một góc bằng 90 độ.
trong 1 tam giác vuông, bình phương cạnh huyền bằng tổng bình vuông 2 cạnh góc vuông
dinh li phát biểu rằng bình phương canh huyen (cạnh đối diện với goc vuong ) bằng tổng bình phương của hai canh ke còn lại.
Định lí pitago là mộ liên hệ căn bản trong hình học giữa ba cạnh tam giác của một tam giác vuông .
Định lí phát biểu rằng bình phương cạnh huyền bằng tổng bình phương hai cạnh kề còn lại