Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
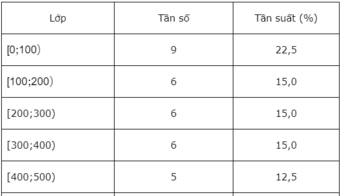
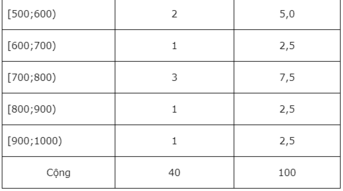
b) b) Cộng các tần suất của bốn lớp [300;400), [400;500), [500;600), [600;700) ta được 15+ 12,5+ 5+ 2,5 = 35. Đáp án là B.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
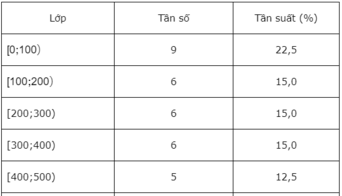
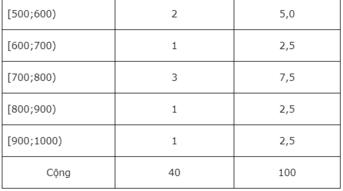
a) a) Nhìn vào bảng ta thấy lớp L 1 có tần số cao nhất. Đáp án là A.

a)Số học sinh giỏi lớp 6a là:
40x22,5%=9(học sinh)
Số học sinh trung bình lớp 6a là:
9x200%=18(học sịnh)
Số học sinh khá lớp 6a là:
40-(9+18)=13(học sinh)
b)Tỉ số phần trăm số học sinh trung binh so với cả lớp là:
18:40%=45(%)
Tỉ số phần trăm số học sinh khá so với cả lớp là:
13:40%=32,5(%)

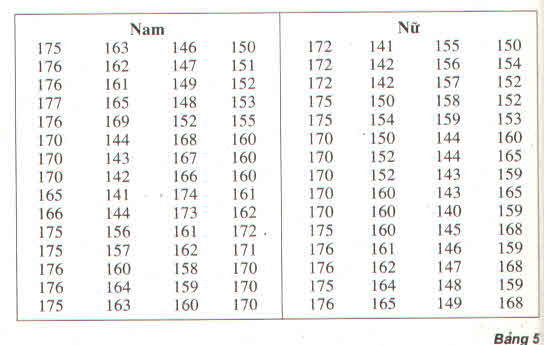
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T

ta thấy:\(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\)
> áp dụng bđt cosi: 1+b2>=2b
>\(a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{ab}{2}\)
cminh tương tự với \(\dfrac{b}{1+c^2};\dfrac{c}{1+b^2}\)
cộng lần lượt 2 vế ta vừa cminh
>bthức tương đương với: a+b+c-\(\dfrac{ab+bc+ca}{2}\ge3-\dfrac{3}{2}=\dfrac{3}{2}\) đpcminh
(vì (a+b+c)2>=3(ab+bc+ca) hay 32>=3(ab+bc+ca)
> ab+bc+ca<=3)

2) a) hình tự vẽ nhé
gọi tọa độ điểm D là \(D\left(x;y\right)\)
ta có : \(\overrightarrow{BC}\left(-1;-1\right)\) ; \(\overrightarrow{AD}=\left(x-2;y+1\right)\)
vì ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{BC}=\overrightarrow{AD}\Rightarrow\left\{{}\begin{matrix}-1=x-2\\-1=y+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\) vậy ...
b) ĐK : \(-2\sqrt{2}\le x\le2\sqrt{2}\)
\(\sqrt{8-x^2}=x^2\) \(\Leftrightarrow x^4=8-x^2\) (bình phương 2 quế )
\(\Leftrightarrow x^4+x^2-8=0\Leftrightarrow\left[{}\begin{matrix}x^2=\frac{-1+\sqrt{33}}{2}\left(N\right)\\x^2=\frac{-1-\sqrt{33}}{2}\left(L\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\sqrt{\frac{-1+\sqrt{33}}{2}}\left(TMĐK\right)\) vậy ...
E chỉ bt sương sương Bài 1 a :((. Chắc ko đúng
\(\left\{{}\begin{matrix}x+y+z=3\\x-z=0\\z=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y+2=3\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\)

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)





Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.