Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu x =3,5 thì |x| = 3,5
nếu x >0 thì | x| = x
nếu x = \(\frac{-4}{7}\) thì |x| = \(\frac{-4}{7}\)
Nếu x=0 thì |x| = 0
Nếu x<0 thì |x| =-X
------------------------------------------------------------------------
a) Nếu x = 3,5 thì \(|x|\)= 3,5
Nếu x = \(\frac{-4}{7}\)thì \(|x|\)= \(\frac{4}{7}\)
b) Nếu x > 0 thì \(|x|\)= x
Nếu x = 0 thì \(|x|\)= 0
Nếu x < o thì \(|x|\)= x
_ hok tốt _

Nếu x > 0 thì |x| = x
Nếu x = 0 thì |x| = 0
Nếu x < 0 thì |x| = -x

Nếu x=3,5 thì |x|=3,5
Nếu x=\(\dfrac{-4}{7}\) thì|x|= \(\dfrac{4}{7}\)
Nếu x>0 thì|x|=x
Nếu x=0 thì|x|=0
Nếu x<0 thì|x|=-x
1a) điền vào chỗ trống(...)
Nếu x = 3,5 thì |x| =..\(3,5\)..
Nếu x = -4/7 thì|x| = ..\(\dfrac{4}{7}\).
Nếu x > 0 thì |x| =...\(x\).
Nếu x = 0 thì |x |=..\(0\)..
Nếu x < 0 thì |x| =.\(-x\)...

Vì \(x< y\Rightarrow\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\) (*)
Thêm ab vào hai vế của (*) : ad + ab < bc + ab
=> a(b+d) < b(a+c)
=> \(\frac{a}{b}< \frac{a+c}{b+d}\)
=> x < z (1)
Thêm cd vào hai vế của (*): ad + cd < bc + cd
=> d(a + c) < c(b + d)
=> \(\frac{a+c}{b+d}< \frac{c}{d}\)
=> z < y (2)
Từ (1) và (2) => x < z < y
Vì x<y⇒ab <cd ⇒ad<bc (*)
Thêm ab vào hai vế của (*) : ad + ab < bc + ab
=> a(b+d) < b(a+c)
=> ab <a+cb+d
=> x < z (1)
Thêm cd vào hai vế của (*): ad + cd < bc + cd
=> d(a + c) < c(b + d)
=> a+cb+d <cd
=> z < y (2)
Từ (1) và (2) => x < z < y

Theo đề bài ta có x = \(\frac{a}{m}\) , y = \(\frac{b}{m}\)( a, b, m \(\in\) Z, m > 0 )
Vì x < y nên ta suy ra a < b
Ta có : x = \(\frac{2a}{2m}\), y = \(\frac{2b}{2m}\), , z = \(\frac{a+b}{2m}\)
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
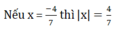
a) 3,5 và 4/7
b)
+ x=x
+ x=0
+ x=-x