Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chứng minh:
∠(IDM) =∠(IDN) (vì DI là tia phân giác của ∠(MDN) (1)
∠(IDM) =∠(EDK) (vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∠(EDK) =∠(IDN) (điều phải chứng minh)

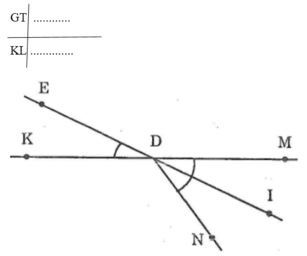
GT: DI là tia phân giác của \(\widehat{MDN}\)
\(\widehat{EDK}\) đối đỉnh với \(\widehat{IDM}\)
KL: \(\widehat{EDK}=\widehat{IDM}\)
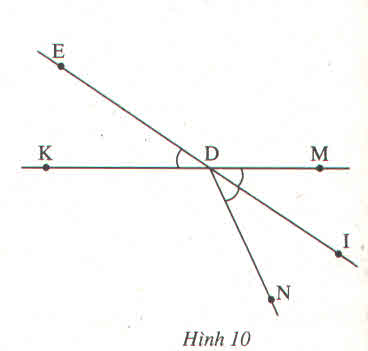
Chứng minh (h.10)
(vì DI là tia phân giác của \(\widehat{MDN}\)) (1)
(vì 2 góc này đối đỉnh) (2)
Từ (1) và (2) suy ra \(\widehat{EDK}=\widehat{IDN}\)
Đó là điều phải chứng minh.


Chứng minh:
\(\widehat{IDM}=\widehat{IDN}\) ( vì \(DI\) là tia pân giác của \(\widehat{MDN}\)) (1)
\(\widehat{IDM}=\widehat{EDK}\) ( hai góc đối đỉnh )
Từ (1) và (2) suy ra : \(\widehat{EDK}=\widehat{IDN}\left(đpcm\right)\)
Chúc bạn học tốt!
Ta có: Chứng minh:IDM=IDN (Vì DI là tia phân giác của MDN ) (1)
Ta có: IDM=EDK (Vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra: EDK=IDN (điều phải chứng minh)

1) đề thiếu nhé
2) Sửa lại : AM | BC
+) Góc A + B + C = 180o => A + 50o + 50o = 180o => A = 80o
=> góc BAM = A/2 = 40o
+) Tam giác BAM có: góc BAM + B + AMB = 180o => 40o + 50o + AMB = 180o => AMB = 90o
=> AM | BC

hình của mjnh thiếu điểm H và K rồi bạn tự thêm vào đi
a, tam giác MND cân tại M (gt)
=> ^MND = ^MDN (tc)
^MND + ^MNB = 180 (kb)
^MDN + ^MDA = 180 (kb)
=> ^MNB = ^MDA
xét tam giác MNB và tam giác MDA có BN = DA (gt)
MN = MD do tam giác MND cân tại M (gt)
=> tg MNB = tg MDA (c-g-c)
=> MA = MB (đn)
=> tg MAB cân tại M (Đn)
b, xét tam giác DHA và tam giác NKB có : AD = BN (gt)
^AHD = ^BKN = 90
^A = ^B do tam giác MAB cân tại M (câu a)
=> tg DHA = tg NKB (ch-gn)
=> DH = KN (đn)
c, tg DHA = tg NKB (câu b)
=> AH = KB (đn)
có MA = MB (câu a)
AH + MH = AM
MK + KB = BM
=> MH = MK
d, có ^HDA = ^KNB do tg DHA = tg NKB (Câu b)
^HDA = ^NDI (đối đỉnh)
^KNB = ^DNI (đối đỉnh)
=> ^NDI = ^DNI
=> tam giác DNI cân tại I