Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

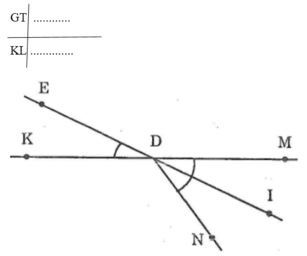
GT: DI là tia phân giác của \(\widehat{MDN}\)
\(\widehat{EDK}\) đối đỉnh với \(\widehat{IDM}\)
KL: \(\widehat{EDK}=\widehat{IDM}\)
Chứng minh (h.10)
ˆIDM=ˆIDNIDM^=IDN^ (vì DI là tia phân giác của \(\widehat{MDN}\)) (1)
ˆIDM=ˆEDKIDM^=EDK^ (vì 2 góc này đối đỉnh) (2)
Từ (1) và (2) suy ra \(\widehat{EDK}=\widehat{IDN}\)


cái đề dài thế này, chả biết khó hay ko nhưng mà ngại làm quá :[
hình như câu b cho đề sai, pải là: ∆EAB=∆ECD mới đúng

GT KL DI là tia phân giác của MDN EDK đối đỉnh với IDM EDK = IDN
Chứng minh:
\(\widehat{IDM}=\widehat{IDN}\) ( vì \(DI\) là tia pân giác của \(\widehat{MDN}\)) (1)
\(\widehat{IDM}=\widehat{EDK}\) ( hai góc đối đỉnh )
Từ (1) và (2) suy ra : \(\widehat{EDK}=\widehat{IDN}\left(đpcm\right)\)
Chúc bạn học tốt!
Ta có: Chứng minh:IDM=IDN (Vì DI là tia phân giác của MDN ) (1)
Ta có: IDM=EDK (Vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra: EDK=IDN (điều phải chứng minh)

A B C M N Q P O R S T A B C H M D I A B C D K G M K E P F (Hình a) (Hình b) (Hình c) Q I
Bài toán 1: (Hình a)
Gọi đường thẳng qua N vuông góc với AN cắt AC tại R, qua P kẻ đường thẳng song song với BC. Đường thẳng này cắt AM,AN,BC lần lượt tại S,T,K.
Ta thấy \(\Delta\)APR có AN vừa là đường cao, đường phân giác => \(\Delta\)APR cân tại A => AP = AR, NP = NR
Áp dụng hệ quả ĐL Thales \(\frac{BM}{PS}=\frac{CM}{KS}\left(=\frac{AM}{AS}\right)\)=> PS = KS
Áp dụng ĐL đường phân giác trong tam giác: \(\frac{TK}{TP}=\frac{AK}{AP}\Rightarrow\frac{ST+SK}{TP}=\frac{AK}{AR}\)
\(\Rightarrow\frac{2ST+PT}{TP}=\frac{AR+RK}{AR}\Rightarrow\frac{2ST}{TP}=\frac{RK}{AR}\)
Dễ thấy NS là đường trung bình của \(\Delta\)RKP => RK = 2NS. Do đó \(\frac{ST}{TP}=\frac{NS}{AR}\)
Đồng thời NS // AR, suy ra \(\frac{ST}{TP}=\frac{NS}{AR}=\frac{SQ}{QA}\)=> QT // AP (ĐL Thaels đảo)
Mà AP vuông góc PO nên QT vuông góc PO. Từ đây suy ra T là trực tâm của \(\Delta\)POQ
=> QO vuông góc PT. Lại có PT // BC nên QO vuông góc BC (đpcm).
Bài toán 2: (Hình b)
Ta có IB = IC => \(\Delta\)BIC cân tại I => ^IBC = ^ICB = ^ACB/2 => \(\Delta\)MCI ~ \(\Delta\)MBC (g.g)
=> MC2 = MI.MB. Xét \(\Delta\)AHC có ^AHC = 900 , trung tuyến HM => HM = MC
Do đó MH2 = MI.MB => \(\Delta\)MIH ~ \(\Delta\)MHB (c.g.c) => ^MHI = ^MBH = ^MBC = ^MCI
=> Tứ giác CHIM nội tiếp. Mà CI là phân giác ^MCH nên (IH = (IM hay IM = IH (đpcm).
Bài toán 3: (Hình c)
a) Gọi đường thẳng qua C vuông góc CB cắt MK tại F, DE cắt BC tại Q, CG cắt BD tại I.
Áp dụng ĐL Melelaus:\(\frac{MB}{MC}.\frac{GA}{GB}.\frac{DC}{DA}=1\)suy ra \(\frac{DC}{DA}=2\)=> A là trung điểm DC
Khi đó G là trọng tâm của \(\Delta\)BCD. Do CG cắt BD tại I nên I là trung điểm BD
Dễ thấy \(\Delta\)BCD vuông cân tại B => BI = CM (=BC/2). Từ đó \(\Delta\)IBC = \(\Delta\)MCF (g.c.g)
=> CB = CF => \(\Delta\)BCF vuông cân ở C => ^CBA = ^CBF (=450) => B,A,F thẳng hàng
=> CA vuông góc GF. Từ đó K là trực tâm của \(\Delta\)CGF => GK vuông góc CF => GK // CM
Theo bổ đề hình thang thì P,Q lần lượt là trung điểm GK,CM. Kết hợp \(\Delta\)CEM vuông ở E
=> EQ=CM/2. Áp dụng ĐL Melelaus có \(\frac{GD}{GM}.\frac{EQ}{ED}.\frac{CM}{CQ}=1\)=> \(\frac{EQ}{ED}=\frac{1}{4}\)
=> \(\frac{ED}{CM}=2\)=> DE = 2CM = BC (đpcm).
b) Theo câu a thì EQ là trung tuyến của \(\Delta\)CEM vuông tại E => EQ = QC => ^QEC = ^QCE
Vì vậy ^PEG = ^QEC = ^QCE = ^PGE => \(\Delta\)EPG cân tại P => PG = PE (đpcm).

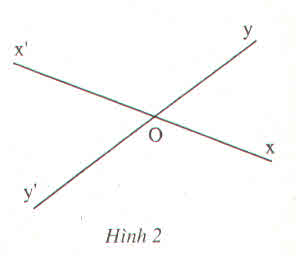
a) Góc xOy và góc .....là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'
ghi ngắn gọn là ( ghi mỗi đáp án)
a) X'OY'
b) là hai góc đối đỉnh
+) Của cạnh OX' và cạnh OY là tia đối của cạnh OY'
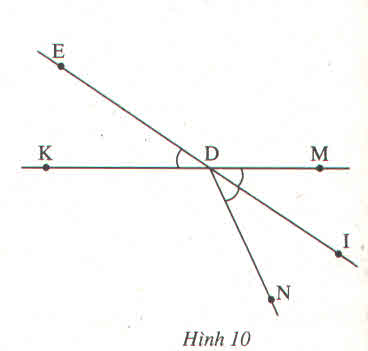




Chứng minh:
∠(IDM) =∠(IDN) (vì DI là tia phân giác của ∠(MDN) (1)
∠(IDM) =∠(EDK) (vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∠(EDK) =∠(IDN) (điều phải chứng minh)