Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Với công suất nơi tiêu thụ là không đổi, để thay đổi hiệu suất của quá trình truyền tải, rõ ràng công suất nơi phát phải thay đổi.
Gọi ∆ P 1 và ∆ P 2 lần lượt là hao phí truyền tải tương ứng với hai trường hợp
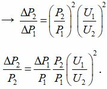
+ Với ![]() Ta có
Ta có 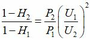
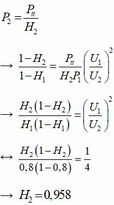

Lời giải:
Vì truyền tải điện năng cần $2$ dây dẫn nên: \(R=\rho\frac{2l}{S}=3\left(\Omega\right)\)
Công suất hao phí: \(\Delta P=I^2R=\left(\frac{P}{U.\cos\varphi}\right)^2R=\frac{250000}{27}W\)
Suy ra hiệu suất truyền tải là \(H=\frac{P-\Delta P}{P}=98,15\%\)
Xin lỗi mình tính nhầm, vẫn công thức như bài giải dưới, kết quả là $94%$

Hao phí truyền tải điện: \(P_{hp}=10\%.P= 0,1.P=20kW=20000W\)
Ta có: \(P_{hp}=I^2.R=I^2.200=20000\Rightarrow I = 10A\)
Chọn A.

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

Chọn đáp án A
+ Khi chưa tăng công suất nơi tiêu thụ ta có: ![]() với
với ![]()
+ Khi tăng công suất nơi tiêu thụ lên 10% ta có:
![]()
![]()
+ Lập tỉ số 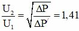

Đáp án D

Giải thích: Đáp án B
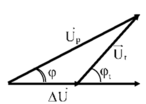
Từ giản đồ vectơ ta có
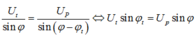
![]()
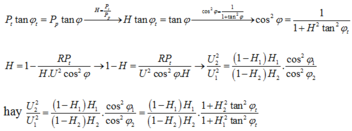
*Áp dụng công thức:
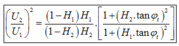
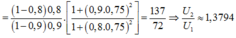
Đáp án C
+ Với công suất nơi tiêu thụ là không đổi, để thay đổi hiệu suất của quá trình truyền tải, rõ ràng công suất nơi phát phải thay đổi.
Gọi ∆ P 1 và ∆ P 2 lần lượt là hao phí truyền tải tương ứng với hai trường hợp
+ Với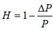 Ta có
Ta có 
mặc khác