Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

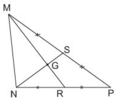
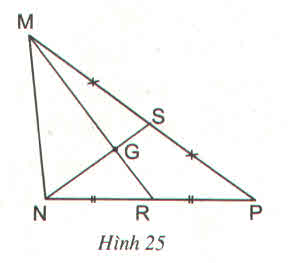
Hình vẽ cho ta biết hai đường trung tuyến MR và NS cắt nhau tại G nên G là trọng tâm của tam giác MNP
Vì vậy ta điền số như sau:
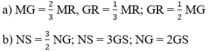
- Ta chứng minh:
G là trọng tâm của tam giác MNP và MR và NS là hai đường trung tuyến.
Nên theo tính chất đường trung tuyến ta có
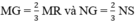
Ta có
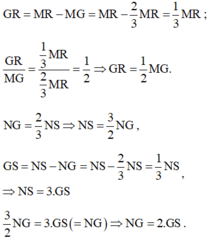

Từ hình vẽ ta thấy: S, R là hai trung điểm của hai đoạn thẳng trong tam giác nên NS và MR là hai đường trung tuyến.
G là giao của hai đường trung tuyến nên G là trọng tâm của ΔMNS, do đó ta có thể điền:
a/ MG =\(\dfrac{2}{3}\) MR , GR=\(\dfrac{1}{3}\) MR , GR=\(\dfrac{1}{2}\) MG
b/NS= \(\dfrac{3}{2}\) NG, NS =\(\dfrac{3}{1}\) GS, NG= \(\dfrac{2}{1}\) GS

a) \(\sqrt{1}=1\)
\(\sqrt{1+2+1}=2\)
\(\sqrt{1+2+3+2+1}=3\)
b) \(\sqrt{1+2+3+4+3+2+1}=4\)
\(\sqrt{1+2+3+4+5+4+3+2+1}=5\)
\(\sqrt{1+2+3+4+5+6+5+4+3+2+1}=6\)

a) \(\sqrt{121}=11\)
\(\sqrt{12321}=111\)
\(\sqrt{1234321}=1111\)
b) \(\sqrt{123454321}=11111\)
\(\sqrt{12345654321}=111111\)
\(\sqrt{1234567654321}=1111111\)

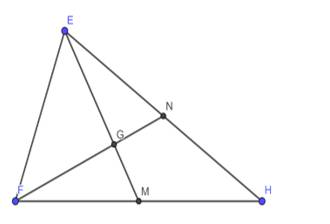
\(\begin{array}{l}EG = \dfrac{2}{3}EM;\,\,\,GM = \dfrac{1}{3}EM;\,\,\,\,GM = \dfrac{1}{2}EG\\FG = 2GN;\,\,\,\,\,FN = 3GN;\,\,\,\,\,\,\,FN = \dfrac{3}{2}FG\end{array}\)

gọi đa thức cần diền vào chỗ (...) là a
`=>11x^2y-a=15x^2y+1`
`=>a=11x^2y-15x^2y-1`
`=>a=-1-4x^2y`
Vậy đa thức cần điền là `-1-4x^2`y
tks bn