Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm: - x 2 + 2 x + 3 = m x ⇔ x 2 + m - 2 x - 3 = 0 1
Dễ thấy (1) luôn có 2 nghiệm phân biệt vì a c = 1 . - 3 = - 3 < 0
Khi đó (d) cắt (P) tại hai điểm phân biệt A x 1 ; m x 1 , B x 2 ; m x 2 , với x 1 , x 2 là nghiệm phương trình (1). Theo Viét, có: x 1 + x 2 = 2 - m , x 1 x 2 = - 3 x 1 x 2 = - 3
I là trung điểm
A B ⇒ I = x 1 + x 2 2 ; m x 1 + m x 2 2 = 2 − m 2 ; − m 2 + 2 m 2
Mà I ∈ ( Δ ) : y = x − 3 ⇒ − m 2 + 2 m 2 = 2 − m 2 − 3 ⇔ m 2 − 3 m − 4 = 0
⇔ m = − 1 = m 1 m = 4 = m 2 ⇒ m 1 + m 2 = 3
Đáp án cần chọn là: D

a) Có thể tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide là một công việc gồm 4 công đoạn, mỗi công đoạn ứng với việc chọn một trong ba loại nucleotide C, G hoặc U cho mỗi vị trí (thứ nhất, thứ hai, thứ ba và cuối cùng) của đoạn. Như vậy, mỗi công đoạn có 3 cách thực hiện. Theo quy tắc nhân, 4 công đoạn có số cách thực hiện là
\(3.3.3.3 = {3^4}\)
Vậy có nhiều nhất \({3^4}\)đoạn phân tử RNA khác nhua cùng có 4 phân tử nucleotide và không có nucleotide A
b)
Có thể tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide là một công việc gồm 4 công đoạn, mỗi công đoạn ứng với việc chọn một trong ba loại nucleotide C, G hoặc U cho mỗi vị trí (thứ nhất, thứ hai, thứ ba và cuối cùng) của đoạn.
Công đoạn thứ nhất: Chọn nucleotide A ở vị trí đầu tiên, có 1 cách chọn
Công đoạn thứ hai: Chọn một trong bốn loại nucleotide A, C, G hoặc U cho mỗi vị trí (thứ hai, thứ 3 và vị trí cuối) của đoạn. Như vậy mỗi công đoạn sau sẽ có 4 cách thực hiện.
Theo quy tắc nhân, 4 công đoạn thực hiện có số cách là
\(1.4.4.4 = {4^3}\)
Vậy có nhiều nhất \({4^3}\)đoạn phân tử RNA khác nhau chứa 4 phân tử nucleotide có nucleotide A nằm ở vị trí đầu tiên.

Tổng số cạnh và đường chéo của đa giác n cạnh là n(n-1)/2, suy ra số đường chéo của đa giác là
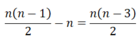
Vì mỗi đường chéo xác định hai vectơ, nên tổng số vectơ là n(n – 3)
Đáp án D

a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).

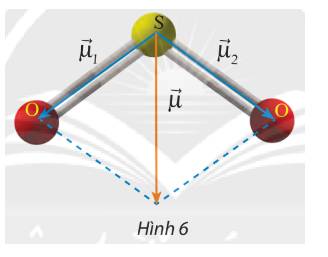
Từ điểm cuối của vectơ \(\overrightarrow {{\mu _1}} \) vẽ vectơ \(\overrightarrow {{\mu _3}} = \overrightarrow {{\mu _2}} \)
Suy ra \(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} \Rightarrow \left| {\overrightarrow \mu } \right| = \left| {\overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} } \right|\)
Ta có: \(\left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _2}} } \right) = 120^\circ \Rightarrow \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right) = 60^\circ \)
\( \Rightarrow {\left| {\overrightarrow \mu } \right|^2} = {\left| {\overrightarrow {{\mu _1}} } \right|^2} + {\left| {\overrightarrow {{\mu _3}} } \right|^2} - 2\left| {\overrightarrow {{\mu _1}} } \right|\left| {\overrightarrow {{\mu _3}} } \right|\cos \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right)\)
\( = 1,{6^2} + 1,{6^2} - 2.1,6.1,6.\cos 60^\circ = \frac{{64}}{{25}}\)
\( \Rightarrow \left| {\overrightarrow \mu } \right| = \sqrt {\frac{{64}}{{25}}} = 1,6\)
Vậy độ dài của \(\overrightarrow \mu \) là 1,6 đơn vị